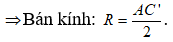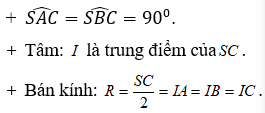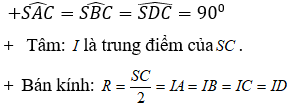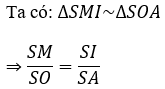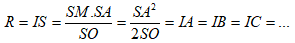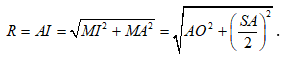Cách xác định Mặt cầu ngoại tiếp, mặt cầu nội tiếp chi tiết
Với Cách xác định Mặt cầu ngoại tiếp, mặt cầu nội tiếp Toán lớp 12 với đầy đủ lý thuyết, phương pháp giải và bài tập có lời giải chi tiết giúp học sinh biết Cách xác định Mặt cầu ngoại tiếp, mặt cầu nội tiếp.
Cách xác định Mặt cầu ngoại tiếp, mặt cầu nội tiếp cực hay
| Mặt cầu ngoại tiếp | Mặt cầu nội tiếp | |
| Hình đa diện | Tất cả các đỉnh của hình đa diện đều nằm trên mặt cầu | Tất cả các mặt của hình đa diện đều tiếp xúc với mặt cầu |
| Hình trụ | Hai đường tròn đáy của hình trụ nằm trên mặt cầu | Mặt cầu tiếp xúc với các mặt đáy và mọi đường sinh của hình trụ |
| Hình nón | Mặt cầu đi qua đỉnh và đường tròn đáy của hình nón | Mặt cầu tiếp xúc với mặt đáy và mọi đường sinh của hình nón |
1. Các khái niệm cơ bản
+ Trục của đa giác đáy: là đường thẳng đi qua tâm đường tròn ngoại tiếp của đa giác đáy và vuông góc với mặt phẳng chứa đa giác đáy.
⇒ Bất kì một điểm nào nằm trên trục của đa giác thì cách đều các đỉnh của đa giác đó.
+ Đường trung trực của đoạn thẳng: là đường thẳng đi qua trung điểm của đoạn thẳng và vuông góc với đoạn thẳng đó.
⇒ Bất kì một điểm nào nằm trên đường trung trực thì cách đều hai đầu mút của đoạn thẳng.
+ Mặt trung trực của đoạn thẳng: là mặt phẳng đi qua trung điểm của đoạn thẳng và vuông góc với đoạn thẳng đó.
⇒ Bất kì một điểm nào nằm trên mặt trung trực thì cách đều hai đầu mút của đoạn thẳng.

2. Cách xác định tâm và bán kính mặt cầu ngoại tiếp của một số hình đa diện cơ bản
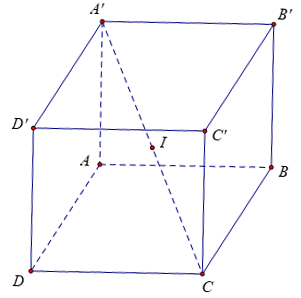
a/ Hình hộp chữ nhật, hình lập phương.
- Tâm: trùng với tâm đối xứng của hình hộp chữ nhật (hình lập phương).
⇒ Tâm là I, là trung điểm của AC'.
- Bán kính: bằng nửa độ dài đường chéo hình hộp chữ nhật (hình lập phương).
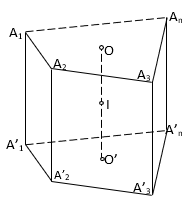
b/ Hình lăng trụ đứng có đáy nội tiếp đường tròn.
Xét hình lăng trụ đứng A1A2A3...An.A'1A'2A'3...A'n, trong đó có 2 đáy A1A2A3...An và A'1A'2A'3...A'n nội tiếp đường tròn (O) và (O'). Lúc đó, mặt cầu nội tiếp hình lăng trụ đứng có:
- Tâm: I với I là trung điểm của OO'
- Bán kính: R = IA1 = IA2 = ... = IAn
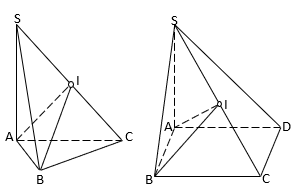
c/ Hình chóp có các đỉnh nhìn đoạn thẳng nối 2 đỉnh còn lại dưới 1 góc vuông.
- Hình chóp S.ABC có:
- Hình chóp S.ABCD có:
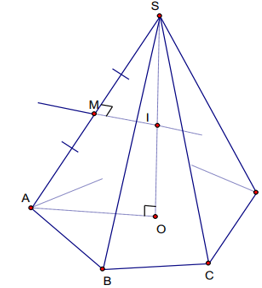
d/ Hình chóp đều.
Cho hình chóp đều S.ABC
- Gọi O là tâm của đáy ⇒ SO là trục của đáy.
- Trong mặt phẳng xác định bởi SO và một cạnh bên, chẳng hạn như mặt phẳng (SAO), ta vẽ đường trung trực của cạnh SA là Δ cắt SA tại M và cắt SO tại I ⇒ I là tâm của mặt cầu.
- Bán kính:
⇒ Bán kính là:
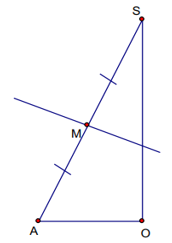
e/ Hình chóp có cạnh bên vuông góc với mặt phẳng đáy.
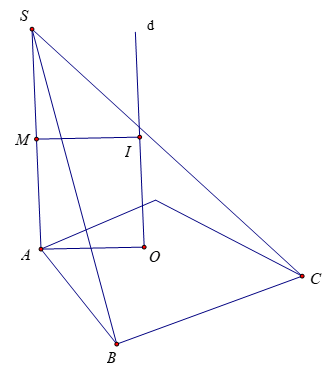
Cho hình chóp S.ABC có cạnh bên SA ⊥ đáy (ABC) và đáy ABC nội tiếp được trong đường tròn tâm O. Tâm và bán kính mặt cầu ngoại tiếp hình chóp S.ABC được xác định như sau:
- Từ tâm O ngoại tiếp của đường tròn đáy, ta vẽ đường thẳng d vuông góc với (ABC) tại O.
- Trong mp(d,SA), ta dựng đường trung trực Δ của cạnh SA, cắt SA tại M, cắt d tại I.
⇒ I là tâm mặt cầu ngoại tiếp hình chóp và bán kính R = IA = IB = IC = IS...
- Tìm bán kính:
Ta có: MIOA là hình chữ nhật.
Xét ΔMAI vuông tại M có:
f/ Hình chóp khác.
- Dựng trục Δ của đáy.
- Dựng mặt phẳng trung trực (α) của một cạnh bên bất kì.
- (α) ∩ Δ = I ⇒ I là tâm mặt cầu ngoại tiếp hình chóp.
- Bán kính: khoảng cách từ đến các đỉnh của hình chóp.
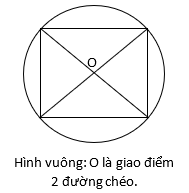
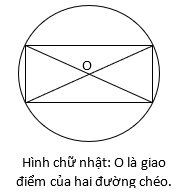
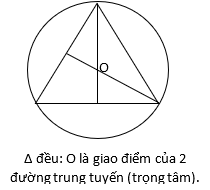
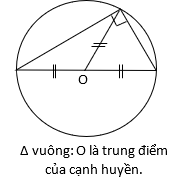
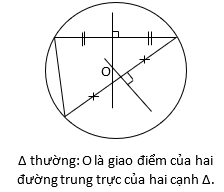
g/ Đường tròn ngoại tiếp một số đa giác thường gặp.
Khi xác định tâm mặt cầu, ta cần xác định trục của mặt phẳng đáy, đó chính là đường thẳng vuông góc với mặt phẳng đáy tại tâm O của đường tròn ngoại tiếp đáy. Do đó, việc xác định tâm ngoại O là yếu tố rất quan trọng của bài toán.