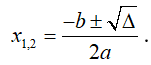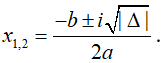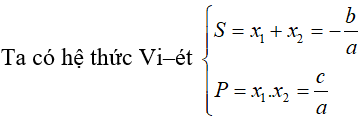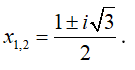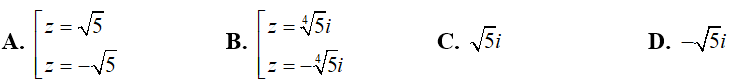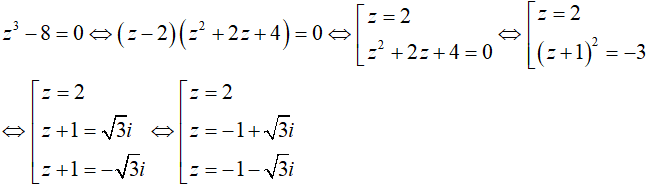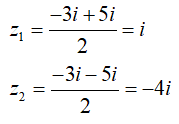Cách giải phương trình bậc 2 số phức

 Phương pháp giải & Ví dụ

- Giải các phương trình bậc hai với hệ số thực

Cho phương trình bậc hai ax² + bx + c = 0( a;b;c ∈ R;a ≠ 0).

Xét Δ = b² - 4ac, ta có

+ Δ = 0 phương trình có nghiệm thực x =  .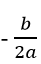

+ Δ > 0 : phương trình có hai nghiệm thực được xác định bởi công thức:

+ Δ < 0 : phương trình có hai nghiệm phức được xác định bởi công thức:

+ Chú ý.

Mọi phương trình bậc n: 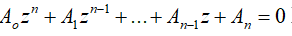 luôn có n nghiệm phức (không nhất thiết phân biệt).

Hệ thức Vi–ét đối với phương trình bậc hai với hệ số thực: Cho phương trình bậc hai ax² + bx + c = 0( a; b;c ∈ R;a ≠ 0 có hai nghiệm phân biệt x₁;x₂ (thực hoặc phức).

- Phương trình quy về phương trình bậc hai với hệ số thực

Phương pháp 1: Phân tích đa thức thành nhân tử:

– Bước 1: Nhẩm 1 nghiệm đặc biệt của phương trình.

+ Tổng các hệ số trong phương trình là 0 thì phương trình có một nghiệm x = 1.

+ Tổng các hệ số biến bậc chẵn bằng tổng các hệ số biến bậc lẻ thì phương trình có một nghiệm x= -1.

– Bước 2: Đưa phương trình về phương trình bậc nhất hoặc bậc hai bằng cách hân tích đa thức ở vế trái của phương trình thành nhân tử (dùng hẳng đảng thức, chia đa thức hoặc sử dụng lược đồ Hoocne) như sau:

Với đa thức f(x) = a_nxⁿ + a_{n - 1}x^{n - 1} + .... + a₁x + a_o chia cho x - a có thương là

g(x) = b_nxⁿ + b_{n - 2}x^{n - 2} + .... + b₁x + b_o dư r

Ví dụ minh họa

– Bước 3: Giải phương trình bậc nhất hoặc bậc hai, kết luận nghiệm

Phương pháp 2: Đặt ẩn phụ:

– Bước 1: Phân tích phương trình thành các đại lượng có dạng giống nhau.

– Bước 2: Đặt ẩn phụ, nêu điều kiện của ẩn phụ (nếu có).

– Bước 3: Đưa phương trình ban đầu về phương trình bậc nhất, bậc hai với ẩn mới.

– Bước 4: Giải phương trình, kết luận nghiệm.

Ví dụ 1:Giải phương trình bậc hai sau: z² - z + 1 = 0

Hướng dẫn:

Ta có a = 1 ; b = -1 ; c = 1 nên Δ = b² - 4ac = -3 < 0

Phương trình có hai nghiệm phức phân biệt là 

Ví dụ 2:Trong C , nghiệm của phương trình z² + √5 = 0 là:

Hướng dẫn:

Chọn đáp án B

Ví dụ 3:Trong C , nghiệm của phương trình z³ - 8 = 0 là :

Hướng dẫn:

Sử dụng hằng đẳng thức số 7, ta có:

Vậy phương trình đã cho có 3 nghiệm phân biệt.

Ví dụ 4:Trong C , phương trình z² + 3iz + 4 = 0 có nghiệm là:

Hướng dẫn:

Ta có : a = 1 ; b = i ; c = 4 nên :

Δ = b² - 4ac = (3i)² - 4.1.4 = -25 <0

Phương trình có hai nghiệm phức là:

Chọn đáp án A.