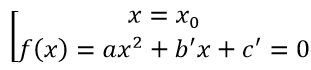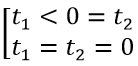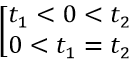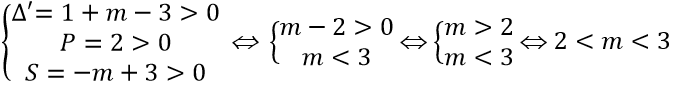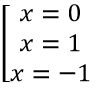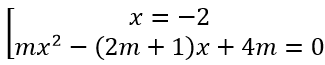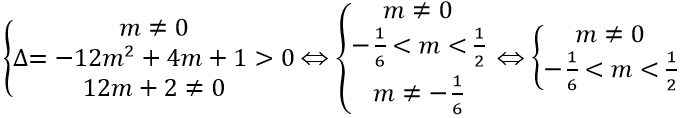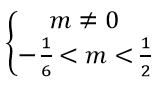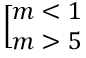Biện luận theo m số giao điểm của đồ thị

A. Phương pháp giải & Ví dụ

Phương pháp cô lập tham số m.

Bước 1: Lập phương trình hoành độ giao điểm dạng F(x,m) = 0 (phương trình ẩn x, tham số m).

Bước 2: Cô lập m đưa phương trình về dạng f(m) = g(x)

Bước 3: Lập bảng biến thiên cho hàm số y = g(x)

Bước 4: Dựa vào yêu cầu bài toán và bảng biến thiên từ đó suy ra m

Phương pháp sử dụng tính chất đặc trưng của phương trình

Phương trình bậc hai y = ax² + bx + c (a ≠ 0)

Phương trình có hai nghiệm phân biệt khi Δ > 0

Phương trình có một nghiệm khi Δ = 0

Phương trình vô nghiệm khi Δ < 0

Phương trình bậc ba y = ax³ + bx² + cx + d = 0(a ≠ 0)

Nếu đã dự đoán được phương trình có một nghiệm x=x_o ta có thể dùng phép chia đa thức hoặc sơ đồ Horner để phân tích thành nhân tử đưa về dạng bậc thấp hơn rồi tìm cách xử lý. Khi đó phương trình bậc ba tương đương với

Dựa vào yêu cầu bài toán, ta đi xử lý phương trình bậc hai f(x).

Nếu không nhẩm được nghiệm và không cô lập được m thì bài toán được giải quyết theo hướng tích hai cực trị, cụ thể:

Đồ thị cắt trục hoành đúng ba điểm phân biệt ⇒ y_CT.y_CĐ < 0

Đồ thị có hai điểm chung với trục hoành ⇒ y_CT.y_CĐ = 0

Đồ thị có một điểm chung với trục hoành ⇒ y_CT.y_CĐ > 0 hoặc hàm số không có cực trị.

Phương trình bậc bốn trùng phương y=ax⁴ + bx² + c = 0(a ≠ 0)(1)

Đặt t = x² (t ≥ 0). Phương trình trở thành at² + bt + c = 0 (2)

Để (1) có đúng một nghiệm thì (2) có hai nghiệm t₁,t₂ thỏa mãn 

Để (1) có đúng một nghiệm thì (2) có hai nghiệm t₁,t₂ thỏa mãn 

Để (1) có đúng một nghiệm thì (2) có hai nghiệm t₁,t₂ thỏa mãn 0=t₁ < t₂

Để (1) có đúng một nghiệm thì (2) có hai nghiệm t₁,t₂ thỏa mãn 0 < t₁ < t₂

Ví dụ minh họa

Ví dụ 1: Tìm m để phương trình y = x⁴ -2x² - m + 3 (1) có bốn nghiệm phân biệt

Hướng dẫn:

Đặt t = x² (t > 0), phương trình (1) trở thành t² - 2t - m + 3 = 0 (2)

Để phương trình (1) có 4 nghiệm phân biệt thì phương trình (1) có hai nghiệm dương phân biệt. Khi đó

Vậy giá trị m cần tìm là 2 < m < 3

Lưu ý: Ta có thể giải bài toán trên bằng phương pháp dùng đồ thị như sau:

Phương trình y = x⁴ - 2x² - m + 3 ⇒ x⁴ - 2x² + 3 = m (1)

Phương trình (1) là phương trình hoành độ giao điểm của hai đường (C): y = x⁴ - 2x² + 3 và đường thẳng d: y = m. Số nghiệm của phương trình (1) bằng số giao điểm của (C) và d

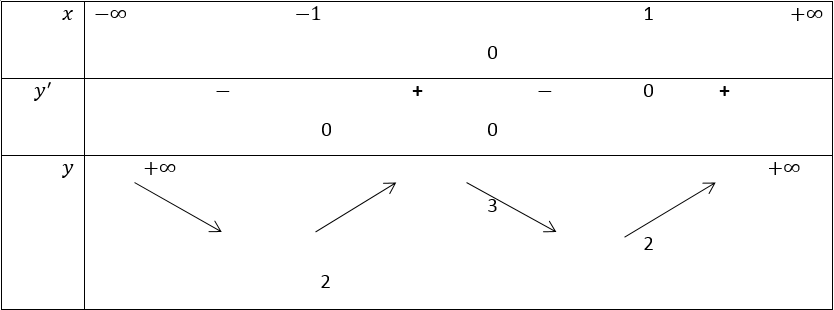
Khảo sát và vẽ bảng biến thiên của hàm số : y = x⁴ -2x² + 3

Tập xác định D = R

Đạo hàm y' = 4x³ - 4x; y' = 0⇒ 

Bảng biến thiên

Dựa vào bảng biến thiên ta thấy (1) có bốn nghiệm phân biệt ⇒ 2 < m < 3

Vậy 2 < m < 3 thỏa mãn yêu cầu bài toán

Ví dụ 2: Cho hàm số y = mx³ - x² - 2x + 8m có đồ thị (C_m). Tìm m để đồ thị (C_m) cắt trục hoành tại 3 điểm phân biệt.

Hướng dẫn:

Phương trình hoành độ giao điểm: mx³ - x² - 2x + 8m = 0

⇒ (x + 2)[mx² - (2m + 1)x + 4m] = 0

(C_m) cắt trục hoành tại 3 điểm phân biệt ⇒ phương trình mx² - (2m + 1)x + 4m = 0 có hai nghiệm phân biệt khác -2.

Vậy giá trị m cần tìm là 

Ví dụ 3: Cho hàm số y= (2x - 1)/(x - 1) có đồ thị (C). Tìm m để đường thẳng (d):y = -x + m cắt đồ thị (C) tại hai điểm phân biệt.

Hướng dẫn:

Phương trình hoành đô giao điểm (2x - 1)/(x - 1) = -x + m (1)

Điều kiện x ≠ 1

Khi đó (1) ⇒ 2x - 1 = (-x + m)(x - 1) ⇒ x² - (m - 1)x + m - 1 = 0 (2)

(d) cắt (C) tại hai điểm phân biệt ⇒ (1) có hai nghiệm phân biệt

⇒ (2) có hai nghiệm phân biệt khác 1

⇒ m² -6m+5>0

Vậy giá trị m cần tìm là m < 1 hoặc m > 5