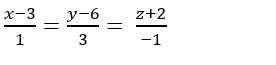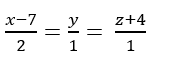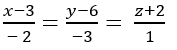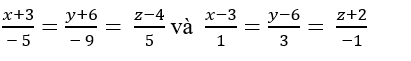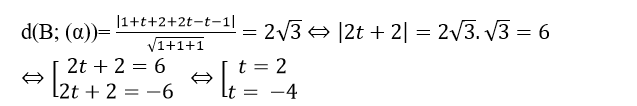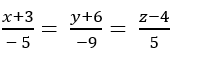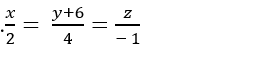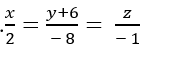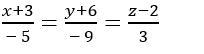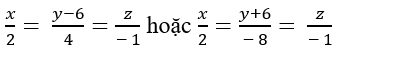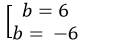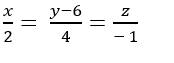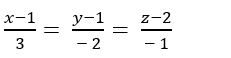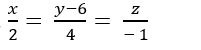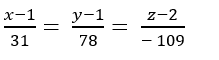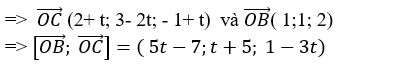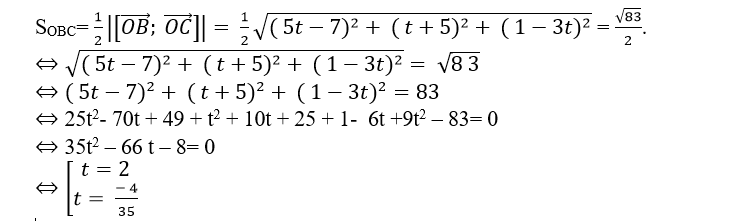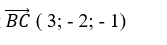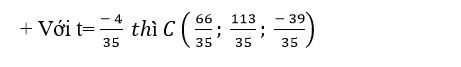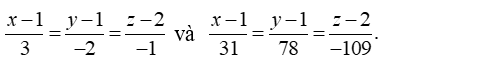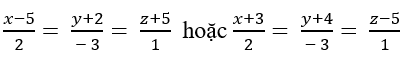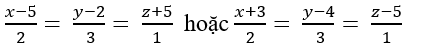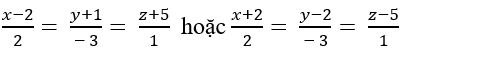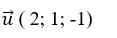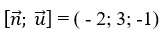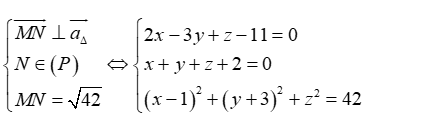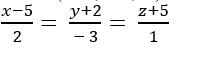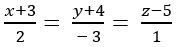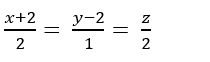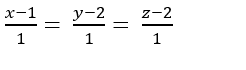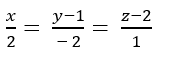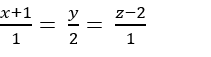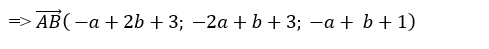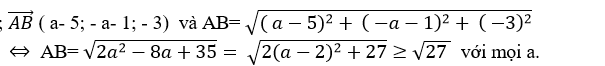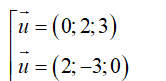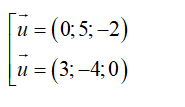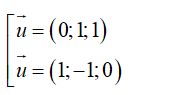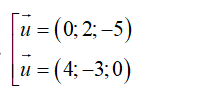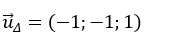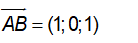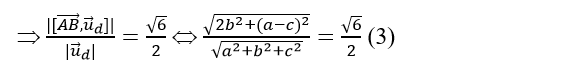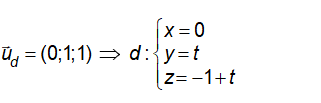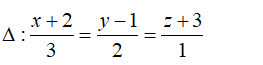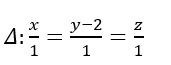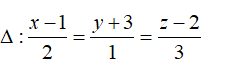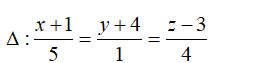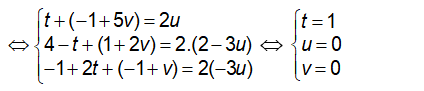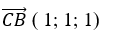Viết phương trình đường thẳng liên quan đến khoảng cách

Ví dụ minh họa

Ví dụ: 1

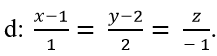
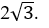
Trong không gian với hệ tọa độ Oxyz; cho đường thẳng  . Viết phương trình đường thẳng Δ đi qua điểm A(2;3; -1) cắt d tại B sao cho khoảng cách từ B đến mặt phẳng (α): x+ y+ z – 1= 0 bằng  .

A. 

B. 

C. 

D. 

Hướng dẫn giải

+ Do điểm B thuộc d nên tọa độ B( 1+ t; 2+ 2t; - t)

Do khoảng cách từ B đến mặt phẳng (α): x+ y+ z – 1= 0 bằng 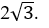 nên:

+ Với t= 2 ta có B(3; 6;-2).

Đường thẳng Δ≡AB: đi qua B(3;6; -2) và nhận vecto 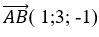 làm vecto chỉ phương

Δ Phương trình Δ: 

+ Với t= -4 ta có B(- 3; - 6;4)

Đường thẳng Δ≡AB đi qua B(- 3;-6;4) và nhận vecto 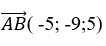 làm vecto chỉ phương

Δ Phương trình Δ: 

Chọn D.

Ví dụ: 2

Trong không gian với hệ tọa độ Oxyz. Viết phương trình đường thẳng Δ đi qua điểm A(-2;2;1) cắt trục tung tại B sao cho OB= 2OA

A.

B.

C.

D. 

Hướng dẫn giải

+ Do B thuộc trục tung Oy nên B(0;b;0)

+ Ta có: 

+ Do OB= 2OA nên |b|=2.3=6 ⇔

+ Với b= 6=> B( 0;6; 0)

Đường thẳng AB qua B( 0;6; 0) và nhận vecto 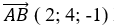 làm vecto chỉ phương

=>Phương trình AB: 

+ Với b= -6 => B (0; - 6; 0)

Đường thẳng AB đi qua B( 0; - 6; 0) và nhận vecto 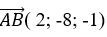 làm vecto chỉ phương

=> Phương trình AB: 

Chọn D.

Ví dụ: 3

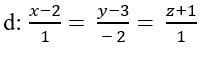
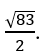
Trong không gian với hệ tọa độ Oxyz. Viết phương trình đường thẳng Δ đi qua điểm B(1;1;2) cắt đường thẳng  tại C sao cho tam giác OBC có diện tích bằng  .

A. 

B. 

C. 

D. Cả A và C đúng

Hướng dẫn giải

+ Điểm C thuộc d nên tọa độ C( 2+ t; 3- 2t; - 1+ t)

+ Diện tích tam giác OBC là:

+ Với t= 2=> C( 4; -1; 1)

Ta có đường thẳng BC: đi qua B( 1; 1; 2) và vecto chỉ phương 

Phương trình BC: 

+ 

Đường thẳng BC: đi qua B( 1; 1; 2) và vecto chỉ phương 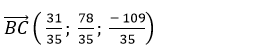 chọn ( 31; 78; -109)

=> Phương trình BC: 

Vậy phương trình của Δ là 

Chọn D

Ví dụ: 4

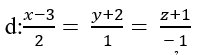
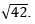
Trong không gian với hệ tọa độ Oxyz cho đường thẳng  , mặt phẳng (P): x+ y+ z+ 2= 0 . Gọi M là giao điểm của d và (P). Gọi Δ là đường thẳng nằm trong (P) vuông góc với d và cách M một khoảng bằng . Phương trình đường thẳng Δ là

A. 

B.

C. 

D. Tất cả sai

Hướng dẫn giải

+ Gọi giao điểm của d và (P) là M

M thuộc d nên M( 3+ 2t; - 2+ t; - 1- t)

Thay tọa độ điểm M vào phương trình mặt phẳng (P) ta được:

3+ 2t - 2+ t- 1- t + 2 = 0

⇔ 2t + 2= 0 ⇔ t= - 1 nên M( 1; -3; 0)

+ Mặt phẳng (P) có vecttơ pháp tuyến  .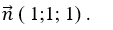

+ Đường thẳng d có vecttơ chỉ phương 

+ Do đường thẳng Δ nằm trong (P) và vuông góc với d nên một vectoc chỉ phương của đường thẳng Δ là: 

+ Gọi N( x; y; z) là hình chiếu vuông góc của M trên Δ, khi đó  .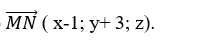

Ta có: 

Giải hệ ta tìm được hai điểm N( 5; - 2; - 5) và N( - 3;– 4; 5).

Với N( 5 ; - 2 ; - 5) , ta có phương trình Δ: 

Với N( -3 ; -4 ; 5) , ta có phương trình Δ: 

Chọn A.

Ví dụ: 5

Trong không gian với hệ tọa độ Oxyz cho hai đường thẳng 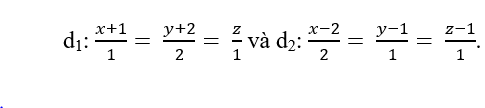 . Đường thẳng d song song với (P): x+ y- 2z + 5= 0 và cắt hai đường thẳng d₁; d₂ lần lượt tại A; B sao cho AB ngắn nhất. Phương trình đường thẳng d là

A. 

B. 

C. 

D. 

Hướng dẫn giải

Gọi giao điểm của đường thẳng d với hai đường thẳng d₁; d₂ lần lượt là A và B.

+ Điểm A thuộc d₁ nên A( - 1+ a; - 2+2a; a)

Điểm B thuộc d₂ nên B( 2+ 2b; 1+ b; 1+ b)

+ Mà đường thẳng d song song với mặt phẳng (P) nên: 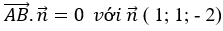 là vecto pháp tuyến của mặt phẳng (P).

=> 1( -a+ 2b+ 3) + 1( -2a+b+ 3) – 2( - a+ b+ 1) = 0

⇔ -a + 2b + 3 – 2a + b+ 3 + 2a- 2b- 2= 0

⇔- a+ b+ 4= 0 hay b= a- 4

Khi đó; 

Dấu “=” xảy ra khi a= 2 => b= 2- 4= - 2

=> A(1; 2; 2) và B( - 2; - 1; - 1)

+ Đường thẳng d: qua điểm A(1;2;2); có vectơ chỉ phương 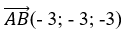 chọn (1;1; 1)

Vậy phương trình của d là 

Chọn B.

Ví dụ: 6

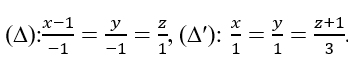
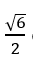
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (α) x+ y- z- 1 = 0 , hai đường thẳng  . Đường thẳng (d) nằm trong mặt phẳng ( α) và cắt (Δ'); (d) và (Δ) chéo nhau mà khoảng cách giữa chúng bằng  có vecto chỉ phương là:

A .

B . 

C . 

D . 

Hướng dẫn giải

+ Mặt phẳng (α) có VTPT 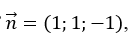 , đường thẳng (Δ) có VTCP 

⇒n→ và u_Δ→ cùng phương nên (Δ) ⊥ (α).

+ Gọi A=(Δ') ⋂ (α)⇒A(0;0;-1) ; B=(Δ)⋂(α)⇒B(1;0;0)⇒ 

+ Vì (d) ⊂(α) và (d) cắt (Δ') nên (d) đi qua A và (Δ) ⊥ (α) nên mọi đường thẳng nằm trong (α) và không đi qua B đều chéo với (Δ).

+ Gọi 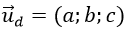 là VTCP của (d) ⇒ u_d→.n→=a+b-c=0 (1) và u_d→ không cùng phương với AB→ (2)

+ Ta có: d(d; Δ) = d( B; d)

Từ (1) và (3)⇒ ac=0 ⇒  .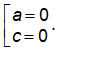

• Với a= 0. Chọn b= c= 1 ⇒

• Với c= 0. Chọn a= 1; b= -1⇒ .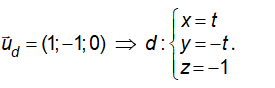

Chọn C.

Ví dụ: 7

Trong không gian với hệ tọa độ Oxyz, cho ba đường thẳng có phương trình 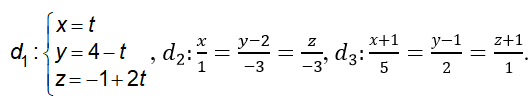 . Viết phương trình đường thẳng Δ, biết Δ cắt ba đường thẳng d₁ ; d₂ ; d₃ lần lượt tại các điểm A, B, C sao cho AB= BC.

A .

B .

C . 

D . 

Hướng dẫn giải

+ Xét ba điểm A, B, C lần lượt nằm trên ba đường thẳng d₁ ; d₂ ; d₃.

Giả sử A(t;4–t;-1+2t),B(u;2–3u;-3u),C(-1+5v;1+2v;-1+v).

+ Ta có: A, B, C thẳng hàng và AB = BC ⇔ B là trung điểm của AC

=> Tọa độ ba điểm A( 1; 3;1); B( 0; 2; 0) và C( - 1;1; -1) .

+ Đường thẳng Δ đi qua B( 0; 2; 0) và có vecto chỉ phương 

=> phương trình đường thẳng 

Chọn B.