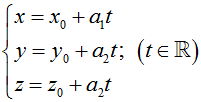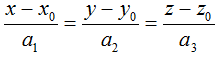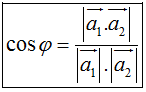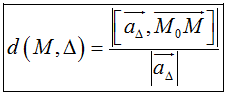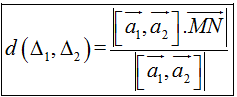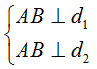Lý thuyết Phương trình đường thẳng trong không gian

A. Tóm tắt lý thuyết

I. Phương trình đường thẳng:

    • Cho đường thẳng Δ đi qua điểm M_o(x_o; y_o; z_o) và nhận vectơ a→ = (a₁; a₂; a₃) với a₁² + a₂² + a₃² ≠ 0 làm vectơ chỉ phương. Khi đó Δ có phương trình tham số là 

    • Cho đường thẳng Δ đi qua điểm M_o(x_o; y_o; z_o) và nhận vectơ a→ = (a₁; a₂; a₃) sao cho a₁a₂a₃ ≠ 0 làm vectơ chỉ phương. Khi đó Δ có phương trình chính tắc là :

II. Góc

1. Góc giữa hai đường thẳng:

    Δ₁ có vectơ chỉ phương a₁→

    Δ₂ có vectơ chỉ phương a₂→

    Gọi φ là góc giữa hai đường thẳng Δ₁ và Δ₂. Ta có:

2. Góc giữa đường thẳng và mặt phẳng:

    Δ có vectơ chỉ phương a_Δ→

    (α) có vectơ chỉ phương n_α→

    Gọi φ là góc giữa hai đường thẳng Δ và α. Ta có:

III. Khoảng cách

1. Khoảng cách từ điểm M đến đường thẳng Δ:

    Δ đi qua điểm M_o và có vectơ chỉ phương a_Δ→

2. Khoảng cách giữa hai đường thẳng chéo nhau:

    Δ₁ đi qua điểm M và có vectơ chỉ phươnga₁→

    Δ₂ đi qua điểm N và có vectơ chỉ phương a₂→

B. Kĩ năng giải bài tập

    Các dạng toán thường gặp

    1. Viết phương trình đường thẳng Δ đi qua hai điểm phân biệt A, B.

    Cách giải:

    Xác định vectơ chỉ phương của Δ là AB→.

    2. Đường thẳng Δ đi qua điểm M và song song với d.

    Cách giải:

    Trong trường hợp đặc biệt:

    • Nếu Δ song song hoặc trùng bới trục Ox thì Δ có vectơ chỉ phương là a_Δ→ = i→ = (1; 0; 0)

    • Nếu Δ song song hoặc trùng bới trục Oy thì Δ có vectơ chỉ phương là a_Δ→ = j→ = (0; 1; 0)

    • Nếu Δ song song hoặc trùng bới trục Oz thì Δ có vectơ chỉ phương là a_Δ→ = k→ = (0; 1; 0)

    Các trường hợp khác thì Δ có vectơ chỉ phương là a_Δ→ = a_d→, với a_d→ là vectơ chỉ phương của d

    3. Viết phương trình đường thẳng Δ đi qua điểm M và vuông góc với mặt phẳng (α).

    Cách giải:

    Xác định vectơ chỉ phương của Δ là a_Δ→ = n_α→, với n_α→ là vectơ pháp tuyến của (α).

    4. Viết phương trình đường thẳng Δ đi qua điểm M và vuông góc với hai đường thẳng d₁, d₂ (hai đường thẳng không cùng phương).

    Cách giải:

    Xác định vectơ chỉ phương của Δ là a_Δ→ = [a₁→, a₂], với a₁→, a₂→ lần lượt là vectơ chỉ phương của d₁, d₂.

    5. Viết phương trình đường thẳng Δ đi qua điểm M vuông góc với đường thẳng d và song song với mặt phẳng (α).

    Cách giải:

    Xác định vectơ chỉ phương của Δ là a_α→ = [a_d→, n_α→], với a_d→ là vectơ chỉ phương của d, n_α→ là vectơ pháp tuyến của (α).

    6. Viết phương trình đường thẳng Δ đi qua điểm A và song song với hai mặt phẳng (α), (β); ((α), (β) là hai mặt phẳng cắt nhau)

    Cách giải:

    Xác định vectơ chỉ phương của Δ là a_Δ→ = [n_α→, n_β→], với n_α→, n_β→ lần lượt là vectơ pháp tuyến của (α), (β).

    7. Viết phương trình đường thẳng Δ là giao tuyến của hai mặt phẳng (α) và (β).

    Cách giải:

    • Lấy một điểm bất kì trên Δ, bằng cách cho một ẩn bằng một số tùy ý.

    • Xác định vectơ chỉ phương của Δ là a_Δ→ = [n_α→, n_β→], với n_α→, n_β→ lần lượt là vectơ pháp tuyến của (α), (β).

    8. Viết phương trình đường thẳng Δ đi qua điểm A và cắt hai đường thẳng d₁, d₂ (A ∉ d₁, A ∉ d₂).

    Cách giải:

    Xác định vectơ chỉ phương của Δ là a_Δ→ = [n₁→, n₂→], với n₁→, n₂→ lần lượt là vectơ pháp tuyến của mp(A, d₁), mp(A, d₂).

    9. Viết phương trình đường thẳng Δ nằm trong mặt phẳng (α) và cắt hai đường thẳng d₁, d₂.

    Cách giải:

    Xác định vectơ chỉ phương của Δ là a_Δ→ = AB→, với A = d₁ ∩ (α), B = d₂ ∩ (α)

    10. Viết phương trình đường thẳng Δ đi qua điểm A, vuông góc và cắt d.

    Cách giải:

    • Xác định B = Δ ∩ d.

    • Viết phương trình đường thẳng Δ đi qua A, B.

    11. Viết phương trình đường thẳng Δ đi qua điểm A, vuông góc với d₁ và cắt d₂, với A ∉ d₂.

    Cách giải:

    • Xác định B = Δ ∩ d₂.

    • Viết phương trình đường thẳng Δ đi qua A, B.

    12. Viết phương trình đường thẳng Δ đi qua điểm A, cắt đường thẳng d và song song với mặt phẳng (α).

    Cách giải:

    • Xác định B = Δ ∩ d.

    • Viết phương trình đường thẳng Δ đi qua A, B.

    13. Viết phương trình đường thẳng Δ nằm trong mặt phẳng (α) cắt và vuông góc đường thẳng d.

    Cách giải:

    • Xác định A = d ∩ (α).

    • Đường thẳng Δ đi qua A và có vectơ chỉ phương của Δ là a_Δ→ = [a_d→, n_α→], với a_d→ là vectơ chỉ phương của d, n_α→ là vectơ pháp tuyến của (α).

    14. Viết phương trình đường thẳng Δ đi qua giao điểm A của đường thẳng d và mặt phẳng (α), nằm trong (α) và vuông góc đường thẳng d (ở đây d không vuông góc với (α)) .

    Cách giải:

    • Xác định A = d ∩ (α).

    • Đường thẳng Δ đi qua A và có vectơ chỉ phương của Δ là a_Δ→ = [a_d→, n_α→], với a_d→ là vectơ chỉ phương của d, n_α→ là vectơ pháp tuyến của (α).

    15. Viết phương trình đường thẳng Δ là đường vuông góc chung của hai đường thẳng chéo nhau d₁, d₂.

    Cách giải:

    • Xác định A = Δ ∩ d₁, B = Δ ∩ d₂ sao cho 

    • Viết phương trình đường thẳng Δ đi qua hai điểm A, B.

    16. Viết phương trình đường thẳng Δ song song với đường thẳng d và cắt cả hai đường thẳng d₁, d₂.

    Cách giải:

    • Xác định A = Δ ∩ d₁, B = Δ ∩ d₂ sao cho AB→, a_d→ cùng phương, với a_d→ là vectơ chỉ phương của d.

    • Viết phương trình đường thẳng Δ đi qua điểm A và có vectơ chỉ phương a_d→ = a_α→.

    17. Viết phương trình đường thẳng Δ vuông góc với mặt phẳng (α) và cắt cả hai đường thẳng d₁, d₂.

    Cách giải:

    • Xác định A = Δ ∩ d₁, B = Δ ∩ d₂ sao cho AB→, n_α→ cùng phương, với n_α→ là vectơ pháp tuyến của (α).

    • Viết phương trình đường thẳng Δ đi qua điểm A và có vectơ chỉ phương a_d→ = n_α→.

    18. Viết phương trình Δ là hình chiếu vuông góc của d lên mặt phẳng (α).

    Cách giải :

    Xác định H ∈ Δ sao cho AH→ ⊥ a_d→,với a_d là vectơ chỉ phương của d.

    • Viết phương trình mặt phẳng (β) chứa d và vuông góc với mặt phẳng (α).

    • Viết phương trình đường thẳng Δ là giao tuyến của hai mặt phẳng (α) và (β)

    19. Viết phương trình Δ là hình chiếu song song của d lên mặt phẳng (α) theo phương d'.

    Cách giải :

    • Viết phương trình mặt phẳng (β) chứa d và có thêm một véc tơ chỉ phương u_d'→.

    • Viết phương trình đường thẳng Δ là giao tuyến của hai mặt phẳng (α) và (β).