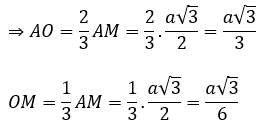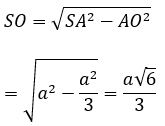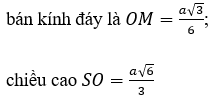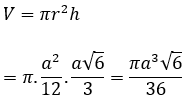Tính chiều cao, bán kính, diện tích, thể tích hình trụ

Cho hình trụ có chiều cao là h và bán kính đáy bằng r, khi đó:

    + Diện tích xung quanh của hình trụ: S_xq = 2πrh

    + Diện tích toàn phần của hình trụ: S_tp = S_xq + S_đ = 2πrh + 2πr²

    + Thể tích khối trụ: V = πr² h

Ví dụ minh họa

Bài 1: Một hình trụ có bán kính đáy r = 5 cm, chiều cao h = 7cm. Tính Diện tích xung quanh, diện tích toàn phần và thể tích của hình trụ.

Hướng dẫn:

Diện tích xung quanh của hình trụ: S_xq = 2πrh = 2π.5.7 = 70π

Diện tích toàn phần của hình trụ: S_tp = 2πrh + 2πr² = 70π+2π.5² = 120π

Thể tích khối trụ: V= πr² h = 2π.5².7 = 350π

Bài 2:

a) Một hình trụ (T) có diện tích toàn phần là 120π (cm²) và có bán kính đáy bằng 6 cm. Tính chiều cao của (T)

b) Một hình trụ (T) có thể tích bằng 81π (cm³) và đường sinh gấp ba lần bán kính đáy. Độ dài đường sinh của (T) là:

Hướng dẫn:

a) Ta có:

S_tp = 2πrh + 2πr² = 2π.6.h + 2π.6² = 120π

⇒ h = 4(cm)

Vậy chiều cao của hình trụ là 4 cm.

b) Gọi bán kính đáy của hình trụ là r

Do đường sinh của hình trụ bằng chiều cao nên chiều cao của hình trụ là 3r

Ta có: V = πr² h = πr².3r = 81π ⇒ r = 3

Vậy độ dài đường sinh là 3.3 = 9 cm.

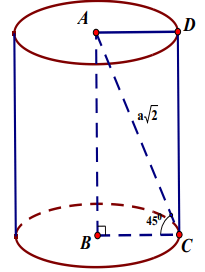
Bài 3: Hình trụ (T) được sinh ra khi quay hình chữ nhật ABCD quanh cạnh AB. Biết AC = a√2 và ∠(ACB)=45^ordm;. Tính diện tích toàn phần S_tp của hình trụ (T)

Hướng dẫn:

Khi quay hình chữ nhật ABCD quanh cạnh AB ta được hình trụ có bán kính đáy BC, đường cao AB

∆ABC vuông cân tại B có AC = a√2 ⇒ AB = BC = a.

S_tp = 2πrh+2πr² = 2π.a.a+2πa² = 4πa²

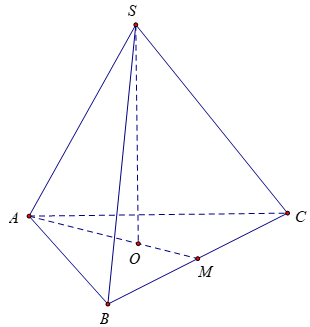
Bài 4: Một hình tứ diện đều ABCD cạnh a. Xét hình trụ có 1 đáy là đường tròn nội tiếp tam giác ABC và có chiều cao bằng chiều cao hình tứ diện. Tính thể tích của hình trụ đó

Hướng dẫn:

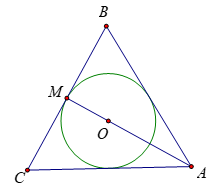
Gọi O là tâm của ∆ABC đều cạnh a, M là trung điểm của BC

Xét tam giác SAO vuông tại O có:

Khi đó, hình trụ có

Thể tích của hình trụ là: