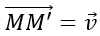Phép dời hình và hai đa diện bằng nhau

Phương pháp giải & Ví dụ

1. Phép dời hình

- Trong không gian quy tắc đặt tương ứng mỗi điểm M với điểm xác định duy nhất được gọi là một phép biến hình trong không gian.

- Phép biến hình trong không gian được gọi là phép dời hình nếu nó bảo toàn khoảng cách giữa hai điểm tùy ý.

Nhận xét:

- Thực hiện liên tiếp các phép dời hình sẽ được một phép dời hình.

- Phép dời hình biến một đa diện thành (H) một đa diện (H’), biến các đỉnh, cạnh, mặt của đa diện (H) thành đỉnh, cạnh, mặt tương ứng của đa diện (H’).

    a) Phép dời hình tịnh tiến theo vector v→ là phép biến hình biến điểm M thành M’ sao cho

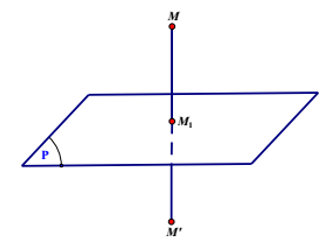
    b) Phép đối xứng qua mặt phẳng (P)

Là phép biến hình biến mọi điểm thuộc (P) thành chính nó biến điểm M không thuộc (P) thành điểm M’ sao cho (P) là mặt phẳng trung trực của MM’.

Nếu phép đối xứng qua mặt phẳng (P) biến hình (H) thành chính nó thì (P) được gọi là mặt phẳng đối xứng của (H).

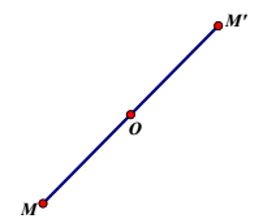
    c) Phép đối xứng tâm O là phép biến hình biến điểm O thành chính nó biến điếm M khác O thành điểm M’ sao cho O là trung điểm của MM’.

Nếu phép đối xứng tâm O biến hình (H) thành chính nó thì O được gọi là tâm đối xứng của (H).

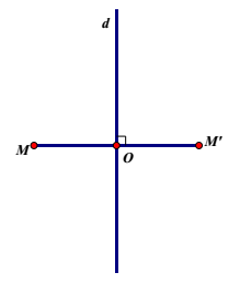
    d) Phép đối xứng qua đường thẳng d là phép biến hình mọi điểm thuộc d thành chính nó, biến điểm M không thuộc d thành điểm M’ sao cho d là trung trực của MM’. Phép đối xứng qua đường thẳng d còn được gọi là phép đối xứng qua trục d.

Nếu phép đối xứng qua đường thẳng d biến hình (H) thành chính nó thì d được gọi là trục đối xứng của (H).

2. Hai đa diện bằng nhau:

Hai đa diện được gọi là bằng nhau nếu có phép dời hình biến đa diện này thành đa diện kia.

Nhận xét:

    + Hai đa diện được gọi là bằng nhau nếu có một phép dời hình biến hình đa diện này thành hình đa diện kia.

    + Hai tứ diện có các cạnh tương ứng bằng nhau thì bằng nhau.