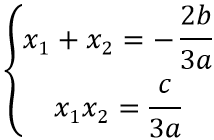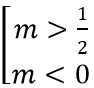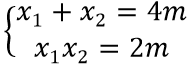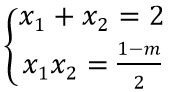Tìm tham số m để hàm số đơn điệu trên đoạn có độ dài l cực hay

A. Phương pháp giải & Ví dụ

Phương pháp giải

Tìm m để hàm số y = ax³ + bx² + cx + d có độ dài khoảng đồng biến (nghịch biến) = l.

   Bước 1: Tính y'=f'(x).

   Bước 2: Tìm điều kiện để hàm số có khoảng đồng biến và nghịch biến: 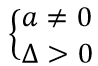 (1).

   Bước 3: Biến đổi |x₁-x₂ | = l thành (x₁+x₂ )² - 4x₁.x₂=l² (2).

   Bước 4: Sử dụng định lý Viét đưa (2) thành phương trình theo m.

   Bước 5: Giải phương trình, so với điều kiện (1) để chọn nghiệm.

Kiến thức cần nhớ

Hàm đa thức bậc ba: y = f(x) = ax³+bx²+ cx + d (a ≠ 0) ⇒ f'(x)=3ax²+ 2bx + c

Sử dụng định lý vi ét cho tam thức bậc hai f'(x)= 3ax² + 2bx + c có

Ví dụ minh họa

Ví dụ 1: Tìm tất cả các giá trị thực của tham số m sao cho hàm số y = 1/3 x³ - 2mx² + 2mx - 3m + 4 nghịch biến trên một đoạn có độ dài là 3.

Hướng dẫn

Ta có f'(x) = x² - 4mx + 2m

Hàm số nghịch biến trên khoảng có độ dài bằng 3 khi và chỉ khi f'(x)= 0 có hai nghiệm phân biệt x₁,x₂ (x₁ < x₂) thỏa mãn |x₁-x₂ |=3

   + f'(x)= 0 có hai nghiệm phân biệt x₁,x₂ ⇔ Δ'= 4m² - 2m > 0 ⇔ 

Theo Vi ét ta có 

   + Với |x₁-x₂ | = 3 ⇔ (x₁ + x₁)² - 4x₁ x₂ - 9 = 0

 (thỏa mãn)

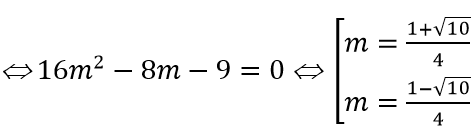
Vậy giá trị của m cần tìm là m=.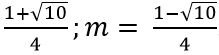

Ví dụ 2: Tìm m để hàm số y = -x³ + 3x² + (m-1)x + 2m - 3 đồng biến trên một khoảng có độ dài nhỏ hơn 1

Hướng dẫn

Ta có f'(x)= -3x² + 6x + m - 1

Hàm số đồng biến trên khoảng có độ dài lớn hơn 1 khi và chỉ khi f'(x) = 0 có hai nghiệm phân biệt x₁,x₂ (x₁ < x₂) thỏa mãn |x₁-x₂ | > 1

   + f'(x)= 0 có hai nghiệm phân biệt x₁,x₂ ⇔ Δ'= 3m + 6 > 0 ⇔ m > -2

Theo Vi ét ta có 

   + Với |x₁-x₂ | > 1 ⇔ (x₁+x₂ )²-4x₁ x₂-1 > 0 ⇔ 4m + 5 > 0 ⇔ m > -5/4

Kết hợp điều kiện ta được m > -5/4

Ví dụ 3: Xác định m để hàm só y = -x⁴ +(m - 2) x² + 1 có khoảng nghịch biến (x₁;x₂) và độ dài khoảng này bằng 1.

Hướng dẫn

Ta có y' = -4x³ + 2(m - 2)x 

Để hàm số có khoảng nghịch biến (x₁;x₂) thì phương trình -2x² + m - 2 = 0 phải có hai nghiệm phân biệt 

Giả sử x₁ < 0 < x₂, khi đó hàm số sẽ nghịch biến trên khoảng (x₁;0) và (x₂; +∞)

Vì độ dài khoảng nghịch biến bằng 1 nên khoảng (x₁;0) có độ dài bằng 1 hay x₁ = -1

Vì -2x² + m - 2 = 0 có một nghiệm là -1 nên -2 + m - 2 = 0 ⇔ m = 4 (thỏa mãn)

Vậy giá trị của tham số m cần tìm là m = 4

B. Bài tập vận dụng

Câu 1: Xác định giá trị của tham số m để hàm số y = f(x) = (m + 1)x³ - 3(m+1)x² + 2mx + 4 đồng biến trên khoảng có độ dài không nhỏ hơn 1.

Câu 2: Xác định giá trị của tham số m để hàm số y = x³ - mx² + (m + 36)x - 5 nghịch biến trên khoảng có độ dài bằng 4√2.

Câu 3: Xác định giá trị của tham số m để hàm số y = x³ + 3x² + mx + m nghịch biến trên đoạn có độ dài nhỏ hơn

Câu 4: Xác định giá trị của tham số m để hàm số y = -x³ + x² - (2 - m)x + 1 nghịch biến trên đoạn có độ dài bằng 2.

Câu 5: Tất cả các giá trị thực của tham số m để hàm số y = 2x³ + 3(m - 1)x² + 6(m - 2)x + 2017 nghịch biến trên khoảng (a;b) sao cho b - a > 3.