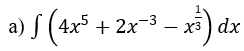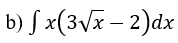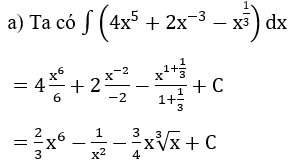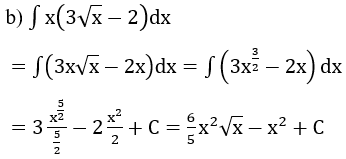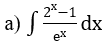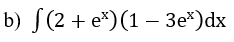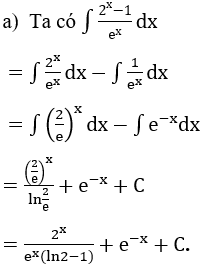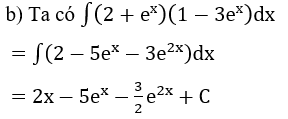Cách tìm nguyên hàm của hàm số chi tiết
Với Cách tìm nguyên hàm của hàm số Toán lớp 12 với đầy đủ lý thuyết, phương pháp giải và bài tập có lời giải chi tiết giúp học sinh biết Cách tìm nguyên hàm của hàm số .
Cách tìm nguyên hàm của hàm số
Phương pháp giải & Ví dụ
I. NGUYÊN HÀM VÀ TÍNH CHẤT
1. Nguyên hàm
Định nghĩa: Cho hàm số f(x) xác định trên K (K là khoảng, đoạn hay nửa khoảng). Hàm số F(x) được gọi là nguyên hàm của hàm số f(x) trên K nếu F'(x) = f(x) với mọi x ∈ K.
Định lí:
1) Nếu F(x) là một nguyên hàm của hàm số f(x) trên K thì với mỗi hằng số C, hàm số G(x) = F(x) + C cũng là một nguyên hàm của f(x) trên K.
2) Nếu F(x) là một nguyên hàm của hàm số f(x) trên K thì mọi nguyên hàm của f(x) trên K đều có dạng F(x) + C, với C là một hằng số.
Do đó F(x)+C, C ∈ R là họ tất cả các nguyên hàm của f(x) trên K. Ký hiệu ∫f(x)dx = F(x) + C.
2. Tính chất của nguyên hàm
Tính chất 1: (∫f(x)dx)' = f(x) và ∫f'(x)dx = f(x) + C
Tính chất 2: ∫kf(x)dx = k∫f(x)dx với k là hằng số khác 0.
Tính chất 3: ∫[f(x) ± g(x)]dx = ∫f(x)dx ± ∫g(x)dx
3. Sự tồn tại của nguyên hàm
Định lí: Mọi hàm số f(x) liên tục trên K đều có nguyên hàm trên K.
4. Bảng nguyên hàm của một số hàm số sơ cấp
| Nguyên hàm của hàm số sơ cấp | Nguyên hàm của hàm số hợp (u = u(x) |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
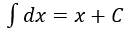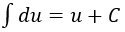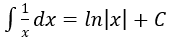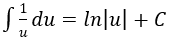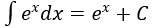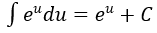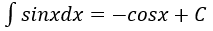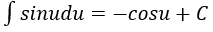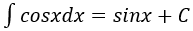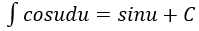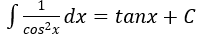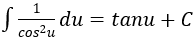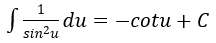II. PHƯƠNG PHÁP TÍNH NGUYÊN HÀM
Phương pháp dùng định nghĩa vá tính chất
+ Biến đổi các hàm số dưới dấu nguyên hàm về dạng tổng, hiệu của các biểu thức chứa x.
+ Đưa các mỗi biểu thức chứa x về dạng cơ bản có trong bảng nguyên hàm.
+ Áp dụng các công thức nguyên hàm trong bảng nguyên hàm cơ bản.
Ví dụ minh họa
Bài 1: Tìm nguyên hàm của hàm số
Hướng dẫn:
Bài 2: Tìm nguyên hàm của hàm số
Hướng dẫn:
Bài viết liên quan
- Cách Giải bất phương trình logarit bằng cách đưa về cùng cơ số chi tiết
- Cách Giải bất phương trình logarit bằng cách đặt ẩn phụ chi tiết
- Cách Tìm nguyên hàm bằng phương pháp đổi biến số chi tiết
- Cách tìm nguyên hàm bằng phương pháp từng phần chi tiết
- Cách Tính tích phân bằng định nghĩa và tính chất chi tiết
