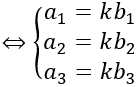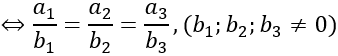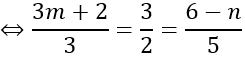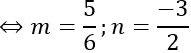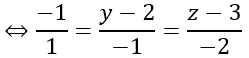Chứng minh hai vecto cùng phương, không cùng phương chi tiết
Với Chứng minh hai vecto cùng phương, không cùng phương Toán lớp 12 với đầy đủ lý thuyết, phương pháp giải và bài tập có lời giải chi tiết giúp học sinh biết Chứng minh hai vecto cùng phương, không cùng phương.
Chứng minh hai vecto cùng phương, không cùng phương
Phương pháp giải & Ví dụ
a→cùng phương với b→ (b→ ≠ 0→ )⇔ a→=k b→ (k∈R)
Ví dụ minh họa
Bài 1: Trong không gian hệ tọa độ Oxyz, cho các vecto a→=(3;2;5),
b→ =(3m+2;3;6-n). Tìm m, n để a→ , b→ cùng phương,
Hướng dẫn:
Ta có: a→=(3;2;5), b→=(3m+2;3;6-n).
a→ , b→ cùng phương
Bài 2: Trong không gian hệ trục Oxyz, cho các điểm A (1; 2; 3), B(2; 1; 1), C (0; 2; 4)
a) Chứng minh A, B, C là 3 đỉnh của một tam giác.
b) Tìm tọa độ điểm M thuộc mặt phẳng Oyz sao cho 3 điểm A, B, M thẳng hàng.
Hướng dẫn:
a) Ta có: AB→=(1; -1; -2), AC→=(-1;0;1)
⇒ AB→, AC→ không cùng phương
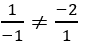
b) M∈(Oyz)⇒M(0;y;z)
AM→ =(-1;y-2;z-3), AB→=(1; -1; -2)
A, B, M thẳng hàng ⇔ AM→, AB→ cùng phương
⇔y=3;z=5
Vậy M (0; 3; 5)
Bài 3: Trong không gian với hệ toạ độ Oxyz, cho tứ giác ABCD có A(2; -1; 5), B(5; -5; 7), C(11; -1; 6), D(5; 7; 2) . Tứ giác ABCD là hình gì?
Hướng dẫn:
AB→=(3; -4;2)
DC→=(6; -8;4)
⇒ DC→=2 AB→ hay DC // AB
⇒ Tứ giác ABCD là hình thang có đáy AB và CD
