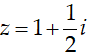Bài tập về Điểm biểu diễn số phức cực hay, chi tiết

Phương pháp giải & Ví dụ

1. Biểu diễn hình học số phức:

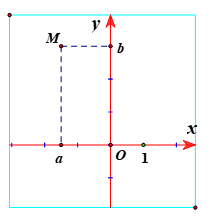
Khái niệm: Điểm M(a;b) biểu diễn cho số phức z = a + bi. Và ngược lại mỗi điểm M(a; b) sẽ biểu diễn số phức z = a + bi.

Chú ý: Để tìm tập hợp điểm biểu diễn các số phức z thỏa mãn điều kiện nào đó ta gọi M(x;y) biểu diễn số phức z rồi dựa vào điều kiện đã cho để tìm một hệ thức liên hệ giữa x;y mà kết luận tập hợp điểm. Nếu

a) ax + by + c = 0 thì tập hợp điểm là đường thẳng

b) (x-a)² + (y-b)² = r²thì tập hợp điểm là đường tròn tâm I(a;b) bán kính r.

Dựa vào biểu diễn hình học của số phức: Điểm M(a;b) biểu diễn cho số phức z=a+bi. Và ngược lại mỗi điểm M(a; b) sẽ biểu diễn số phức z = a + bi.

Ví dụ minh họa

Ví dụ 1:Số phức z = 2 - 3i có điểm biểu diễn trên mặt phẳng tọa độ là:

A. M(2;3).        B. M(-2;-3).        C. M(2; -3).        D. M(-2;3)

Hướng dẫn:

Chọn C.

Ví dụ 2:Cho số phức z = 2 - 3i. Điểm biểu diễn số phức liên hợp của z là

A.(2;3) .        B. (-2;-3).        C. (2;-3).        D.(-2;3)

Hướng dẫn:

Vì z = 2 - 3i nên z = 2 + 3i.

Điểm biểu diễn của z có tọa độ (2;3).

Chọn A.

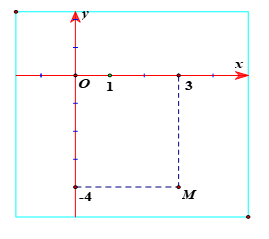
Ví dụ 3:Trên mặt phẳng tọa độ Oxy cho điểm M trong hình vẽ bên là điểm biểu diễn của số phức z. Tìm z?

A. z = -4 + 3i.         B. z = 3 + 4i.

C. z = 3 - 4i.         D. Z = -3 + 4i.

Hướng dẫn:

Ta có M(-3;4).

Vậy điểm M biểu diễn cho số phức z = 3 - 4i

Chọn C

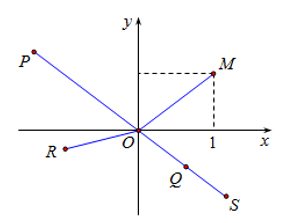
Ví dụ 4:Cho số phức z có điểm biểu diễn là M. Biết rằng số phức 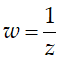 được biểu diễn bởi điểm N gần với một trong bốn điểm , , , như hình vẽ bên.

Hỏi điểm N gần với điểm nào nhất?

A. S         B.Q

C.P         D.R

Hướng dẫn:

Cách 1: (Trắc nghiệm).

Ta có: z = a + bi theo hình vẽ có a = 1; 0 < b < 1 , a = 1, 0 < b < 1 nên ta chọn 

Suy ra: 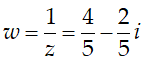 và điểm cần tìm là Q.

Ta có: z = a + bi theo hình vẽ có a = 1 ; 0< b < 1

Ta có: 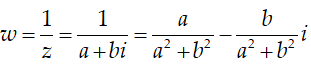 có phần thực dương bé hơn 1 , phần ảo âm lớn hơn -1 nên ta chọn điểm Q là điểm cần tìm.

Chọn B.

Ví dụ 5:

a) Cho số phức z=6+8i. Số phức đối của z có tọa độ điểm biểu diễn là

A.(6; 8)        B.(6;-8)        C.(8; -6).        D.(-6; -8)

b) Điểm M(2;-4) là điểm biểu diễn của số phức

A. z = 2 + 4i        B. 2 - 4i        C. z = -2i        D. z = 4

Hướng dẫn:

a ) z = 6 + 8i nên số phức đối của z là w= -z = -6 - 8i

Vậy điểm biểu diễn của –z là (-6; -8)

Chọn đáp án D.

b) z = a + bi có điểm biểu diễn là M(a;b).

Ta suy ra z = 2 - 4i

Vậy chọn đáp án B.