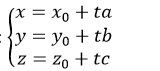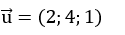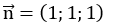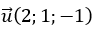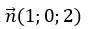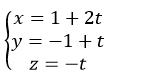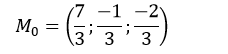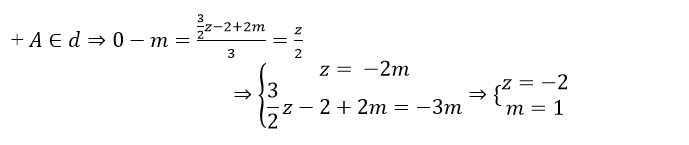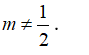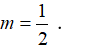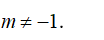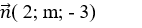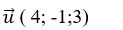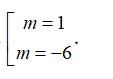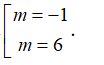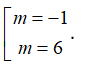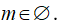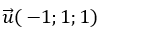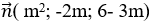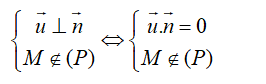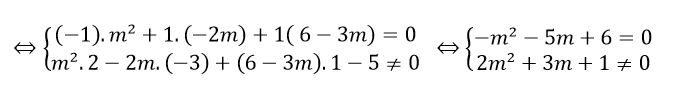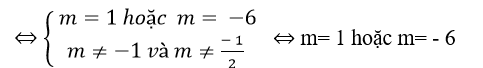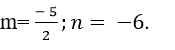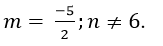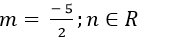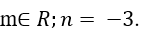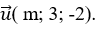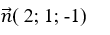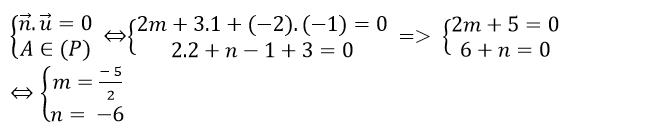Vị trí tương đối của đường thẳng và mặt phẳng

A. Phương pháp giải

Cho đường thẳng d đi qua M_0 (x_0,y_0,z_0 ) và có vectơ chỉ phương 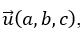 , cho mặt phẳng (P) có phương trình tổng quát là: Ax + By + Cz + D = 0

Gọi 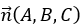 là vectơ pháp tuyến của (P). Để xét vị trí tương đối giữa đường thẳng d và mặt phẳng (P) ta có cách sau:

Cách 1:

Xét tích vô hướng n→.u→ và thay tọa độ điểm M_0 vào phương trình của (P) để kiểm tra, ta có các trường hợp sau:

- n→.u→ ≠ 0⇔d cắt (P)

-n→=ku→⇔d vuông góc với (P)

Cách 2:

Viết phương trình tham số của đường thẳng d: 

Thay x, y, z ở phương trình tham số trên vào phương trình tổng quát của mặt phẳng (P): Ax + By + Cz + D = 0 ta được:

A_(x0+ta)+B_(y0+tb)+C_(z0+tc) +D=0 hay mt+n=0 (1)

Xét số nghiệm t của phương trình (1) ta có các trường hợp sau:

- (1) vô nghiệm ⇔d song song với (P)

- (1) có một nghiệm t = t_0 ⇔d cắt (P) tại điểm M₀(x₀+t₀a;y₀+t₀b;z₀+t₀c)

- (1) có vô số nghiệm ⇔d nằm trong (P)

- (A; B; C) = k (a; b; c) ⇔d vuông góc với (P)

B. Ví dụ minh họa

Ví dụ: 1

Xét vị trí tương đối của đường thẳng 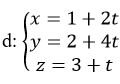 với mặt phẳng sau: (P): x + y + z + 2 = 0

A. Cắt nhau

B. (P) chứa d

C. Song song

D. Vuông góc

Hướng dẫn giải

Đường thẳng d đi qua M_0(1; 2; 3) và có vectơ chỉ phương

Mặt phẳng (P) có vectơ pháp tuyến là: 

Ta có: n→.u→=2+4+1=7 ≠ 0.

Vậy d cắt (P).

Chọn A.

Ví dụ: 2

Xét vị trí tương đối của đường thẳng 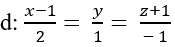 với mặt phẳng (P): x+ 2z – 7 = 0?

A. Cắt nhau

B. song song

C. (P) chứa d

D.Vuông góc

Hướng dẫn giải

+ đường thẳng d đíqua điểm A( 1; 0; -1) và có vecto chỉ phương 

+ Mặt phẳng ( P) có vecto pháp tuyến 

=> n→.u→ = 2. 1+ 0.1- 1.2= 0 và điểm A không thuộc mặt phẳng (P)

=> đường thẳng d song song với mặt phẳng (P)

Chọn B.

Ví dụ: 3

Cho đường thẳng 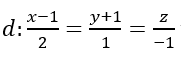 và mặt phẳng (P): x + 2y + z – 1 = 0. Tìm mệnh đề đúng ?

A. d cắt (P) tại điểm có hoành độ 7/3

B.d cắt (P) tại điểm có tung độ (-2)/3

C. d và (P) không có điểm chung .

D. Tất cả sai.

Hướng dẫn giải

Phương trình tham số của d là:

Thay x, y, z vào phương trình tổng quát của (P) ta có:

(1+ 2t) + 2 (-1+t) + (-t) – 1 = 0 (1)

⇔ 3t = 2 nên t = 2/3

Phương trình (1) có 1 nghiệm t = 2/3. Vậy d cắt (P) tại điểm:

Chọn A.

Ví dụ: 4

Xét vị trí tương đối của đường thẳng d với mặt phẳng (P) biết 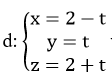 và (P): x + z + 5 = 0?

A. Cắt nhau

B. (P) chứa d

C. Vuông góc

D. Song song

Hướng dẫn giải

Thay x, y, z trong phương trình tham số của đường thẳng d vào phương trình tổng quát của mặt phẳng (P) ta được:

( 2-t) + (2+t) + 5 = 0 ⇔ 0t + 9 = 0 ⇔ 0.t= -9

=> Phương trình vô nghiệm .

Vậy d // (P).

Ví dụ: 5

Xét vị trí tương đối của đường thẳng 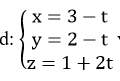 và mặt phẳng (P): x + y + z – 6 = 0

A. (P) chứa d

B. Cắt nhau

C. Song song

D. Vuông góc

Hướng dẫn giải

Thay x, y, z trong phương trình tham số của đường thẳng d vào phương trình tổng quát của mặt phẳng (P) ta được:

(3-t) + (2-t) + (1+2t) – 6 = 0 hay 0t = 0

Phương trình luôn thỏa mãn với mọi t.

Vậy (P) chứa d.

Chọn A.

Ví dụ: 6

Trong không gian Oxyz, cho mặt phẳng (P): x- 2y+ 3z – 4= 0 và đường thẳng 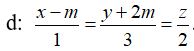 . Với giá trị nào của m thì giao điểm của đường thẳng d và mặt phẳng (P) thuộc mặt phẳng (Oyz) .

A. m= 2

B. m= -1

C.m= 1

D.m= 3

Hướng dẫn giải

Ta có: d∩(P)=A( x; y; z) .

A thuộc mặt phẳng (Oyz) nên x= 0 => A( 0; y;z)

Lại có; A thuộc ( P) nên: 0- 2y+ 3z- 4= 0 ⇔ 

Chọn A.

Ví dụ: 7

Trong không gian Oxyz, cho mặt phẳng (P): 2x+ my – 3z + m- 2= 0 và đường thẳng 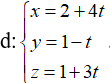 . Với giá trị nào của m thì d cắt (P)

A. 

B. m= 1

C.

D.

Hướng dẫn giải

Mặt phẳng (P) có vecto pháp tuyến 

Đường thẳng d có vecto chỉ phương 

Đường thẳng d cắt (P) ⇔ n→.u→ ≠ 0 ⇔ 2.4+ m.(-1)– 3.3 ≠ 0 hay -m-1 ≠ 0 nên m ≠ -1

Chọn D

Ví dụ: 8

Trong không gian Oxyz, cho đường thẳng 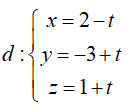 và mặt phẳng (P): m²x- 2my + (6-3m)z- 5= 0. Tìm m để d// (P)

A. 

B. 

C. 

D. 

Hướng dẫn giải

Ta có đường thẳng d đi qua M( 2; -3; 1) và có vecto chỉ phương 

Mặt phẳng (P) có vecto pháp tuyến 

Để d song song với (P) thì m₂x- 2my + (6-3m)z- 5= 0.

Chọn A.

Ví dụ: 9

Trong không gian với hệ tọa độ Oxyz, cho đường thẳng 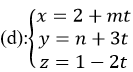 và mặt phẳng (P): 2x+ y- z+ 3= 0. Xác định giá trị của m;n sao cho (P) chứa d?

A.

B.

C.

D.

Hướng dẫn giải

+ Đường thẳng d đi qua A( 2; n; 1) và có vecto chỉ phương 

+ Mặt phẳng (P) có vecto pháp tuyến 

+ Để mặt phẳng (P) chứa d khi và chỉ khi:

Chọn A.