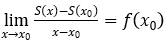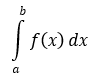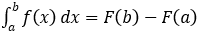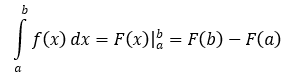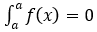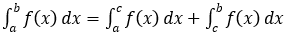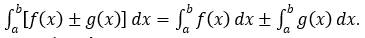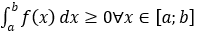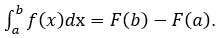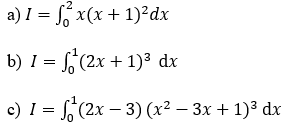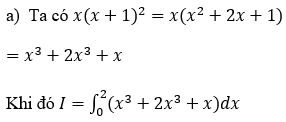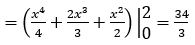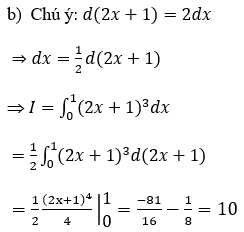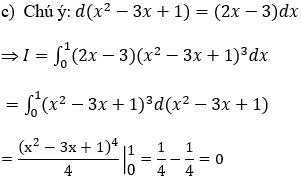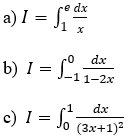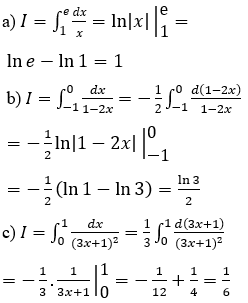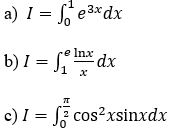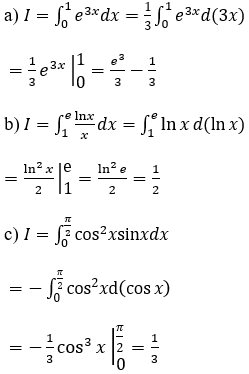Cách Tính tích phân bằng định nghĩa và tính chất chi tiết
Với cách Tính tích phân bằng định nghĩa và tính chất Toán lớp 12 với đầy đủ lý thuyết, phương pháp giải và bài tập có lời giải chi tiết giúp học sinh biết cách Tính tích phân bằng định nghĩa và tính chất .
Tính tích phân bằng định nghĩa và tính chất cực hay
Phương pháp giải & Ví dụ
I. KHÁI NIỆM TÍCH PHÂN
1. Diện tích hình thang cong
• Giới thiệu cho học sinh về cách tính diện tích của một hình thang cong
• Từ đó suy ra công thức:
2. Định nghĩa tích phân
• Cho hàm f liên tục trên một khoảng K và a, b là hai số bất kỳ thuộc K. Nếu F là một nguyên hàm của f trên K thì hiệu số: F(b) – F(a) được gọi là tích phân của f đi từ a đến b, ký hiệu là:
Có nghĩa là: 
• Gọi F(x) là một nguyên hàm của f(x) và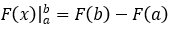 
thì:
Trong đó:
a: là cận trên, b là cận dưới
f(x) gọi là hàm số dưới dấu tích phân
dx: gọi là vi phân của đối số
f(x)dx: Gọi là biểu thức dưới dấu tích phân
II. TÍNH CHẤT CỦA TÍCH PHÂN
Giả sử cho hai hàm số f và g liên tục trên K, a, b, c là ba số bất kỳ thuộc K. Khi đó ta có:
1) 
2) 
(Gọi là tính chất đổi cận)
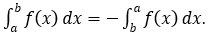
3) 
4)
(Tích phân của một tổng hoặc hiệu hai tích phân bằng tổng hoặc hiệu hai tích phân).
5) 
(Hằng số k trong dấu tích phân, có thể đưa ra ngoài dấu tích phân được)
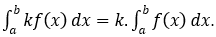
Ngoài 5 tính chất trên, người ta còn chứng minh được một số tính chất như sau:
6) Nếu f(x) ≥ 0∀x ∈ [a;b] thì:
7) Nếu: ∀x ∈ [a;b]: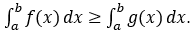 
(Bất đẳng thức trong tích phân)
8) Nếu: ∀x ∈ [a;b] và với hai số M, N ta luôn có: M ≤ f(x) ≤ N. Thì: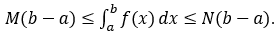
(Tính chất giá trị trung bình của tích phân)
III. PHƯƠNG PHÁP GIẢI TOÁN
Để tính tích phần từ a đến b, ta tiến hành tìm nguyên hàm dựa vào bảng nguyên hàm rồi sau đó thay cận vào theo công thức
Ví dụ minh họa
Bài 1: Tính tích phân
Hướng dẫn:
Bài 2: Tính tích phân
Hướng dẫn:
Bài 3: Tính tích phân
Hướng dẫn:
