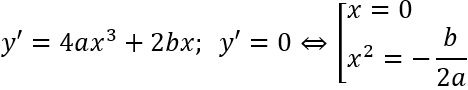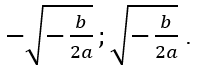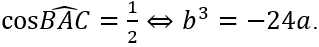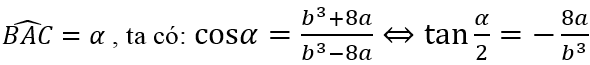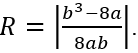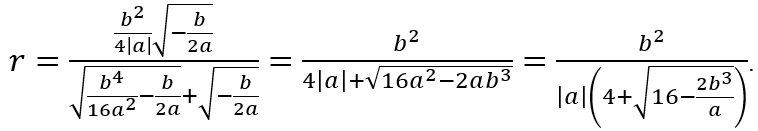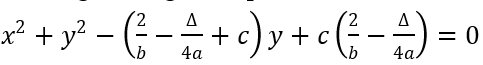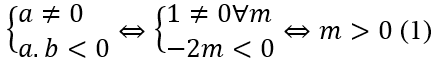Cách giải các dạng bài về cực trị của hàm số cực hay

A. Phương pháp giải & Ví dụ

Phương pháp giải

1. Cực trị của hàm số bậc ba

Hàm số có cực trị y' = 0 có hai nghiệm phân biệt .

Nếu hàm số y = ax³ + bx² + cx + d(a ≠ 0) có hai điểm cực trị x₁,x₂ và

y = g(x).y^' + a.x + b thì đường thẳng đi qua hai điểm cực trị có phương trình y = ax + b và giá trị cực trị là của hàm số là y₁ = a.x₁+b; y₂ = a.x₂ + b

Tìm điều kiện cuả tham số để hàm số có cực trị thỏa mãn hệ thức cho trước

    - Tìm điều kiện để hàm số có cực trị.

   - Phân tích hệ thức để áp dụng vi-et cho phương trình bậc hai.

2. Cực trị của hàm số bậc bốn trùng phương

Cho hàm số: y = ax⁴ + bx² + c (a ≠ 0) có đồ thị là (C).

(C)có ba điểm cực trị y' = 0 có 3 nghiệm phân biệt ⇔ -b/2a > 0 ⇔ ab < 0.

Khi đó hàm số có 3 điểm cực trị thì 3 điểm cực trị là 0;

Tọa độ 3 điểm cực trị tương ứng của đồ thị hàm số là: 

Nhận xét: tam giác ABC cân tại A, có A ∈Oy ;

Tam giác ABC vuông tại 

hoặc ΔABC vuông cân tại A ⇔ BC² = AB² + AC²

Tam giác ABC đều 

hoặc ΔABC đều ⇔ BC² = AB²

Đặc biệt: Tam giác ABC có một góc bằng 120° 

Bán kính đường tròn ngoại tiếp tam giác ABC là 

Bán kính đường tròn nội tiếp tam giác ABC là

Phương trình đường tròn ngoại tiếp ΔABC là:

Ví dụ minh họa

Ví dụ 1. Cho hàm số y = x³ - 3(m + 1)x² + 9x - 2m² + 1 (C). Tìm giá trị của m để đồ thị hàm số (C) có cực đại, cực tiểu tại x₁, x₂ sao cho |x₁ - xc | = 2

Hướng dẫn

Ta có y' = 0 ⇔ x² - 2(m + 1)x + 3 = 0. ĐK có 2 điểm cực trị Δ' = (m + 1)² - 3 > 0

Khi đó

Ví dụ 2. Cho hàm số 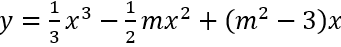 (C). Tìm giá trị của m để đồ thị hàm số (C) có cực đại, cực tiểu tại x₁,x₂ sao cho x₁² + x₂² = 6

Hướng dẫn

Ta có y' = x² - mx + m² - 3. ĐK có 2 cực trị Δ = m² - 4(m² - 3) = 12 - 3m² > 0

Khi đó 

Ví dụ 3. Tìm tất cả các giá trị thực của tham số m sao cho đồ thị hàm số y = x⁴ - 2mx² + 2m⁴ - m có ba điểm cực trị đều thuộc các trục tọa độ.

Hướng dẫn

Ta có y' = 4x³ - 4mx = 4x[x² - m].

Hàm số đã cho có ba điểm cực trị khi và chỉ khi:

Khi đó ba điểm cực trị của đồ thị hàm số là:

A(0; 2m⁴ - m), B(-√m; 2m⁴ - m² - m), C(√m; 2m⁴ - m² - m)

Có A 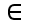Oy.Khi đó ba điểm cực trị đều thuộc các trục tọa độ

⇔ y_B = 0 = y_C ⇔ 2m⁴ - m² - m = 0 ⇔ m = 1

B. Bài tập vận dụng

Câu 1:Cho hàm số y = 4x³ + mx² - 3x + 1. Tìm tất cả các giá trị của m để hàm số có hai điểm cực trị x₁,x₂ thỏa x₁ = -2x₂

Câu 2:Cho hàm số y = (m + 2)x³ + 3x² + mx - 5, m là tham số. Tìm các giá trị của m để các điểm cực đại, cực tiểu của đồ thị hàm số đã cho có hoành độ là các số dương.

Câu 3:Cho hàm số y = x³ + (1 - 2m)x² + (2 - m)x + m + 2 (1). Tìm các giá trị của m để đồ thị hàm số (1) có điểm cực đại, điểm cực tiểu , đồng thời hoành độ của điểm cực tiểu nhỏ hơn 1.

Câu 4:Cho hàm số y = x³ + 3x² + mx + m - 2 (m là tham số) có đồ thị là (Cm). Xác định m để (Cm) có các điểm cực đại và cực tiểu nằm về hai phía đối với trục hoành.

Câu 5:Tìm các giá trị của tham số m để đồ thị hàm số y = 2x³ + 3(m - 3)x² + 11 - 3m có hai điểm cực trị. Đồng thời hai điểm cực trị đó và điểmC(0; -1) thẳng hàng .

Câu 6:Tìm m để hàm số y = x⁴ - 2m² x² + 1 có 3 điểm cực trị là 3 đỉnh của một tam giác vuông cân

Câu 7:Tìm tất cả các giá trị của tham số thực m để đường thẳng qua 2 điểm cực trị của đồ thị hàm số: y = x³ - 3mx + 2 cắt đường tròn tâm I(1;1) bán kính bằng 1 tại 2 điểm A,B mà diện tích tam giác IAB lớn nhất .

Câu 8:Tìm tất cả các giá trị thực của tham số mđể đồ thị hàm số y = 2x³ - 3(m + 1)x² + 6mx có hai điểm cực trị A, B sao cho đường thẳng AB vuông góc với đường thẳng : y = x + 2.