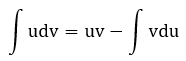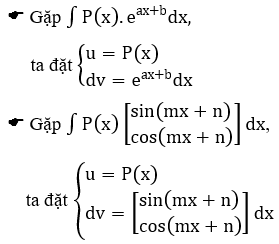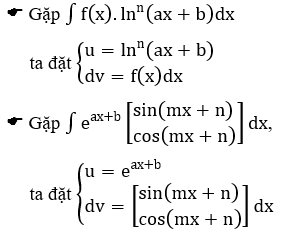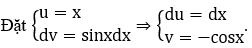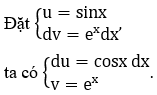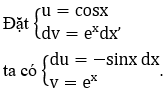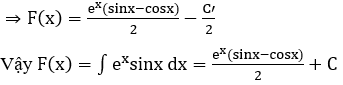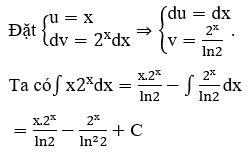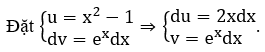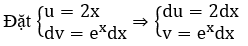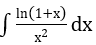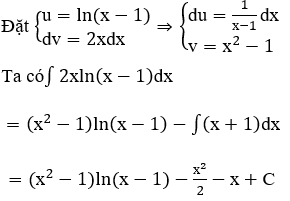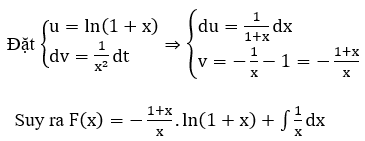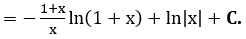Cách tìm nguyên hàm bằng phương pháp từng phần chi tiết
Với Cách tìm nguyên hàm bằng phương pháp từng phần Toán lớp 12 với đầy đủ lý thuyết, phương pháp giải và bài tập có lời giải chi tiết giúp học sinh biết Cách tìm nguyên hàm bằng phương pháp từng phần .
Cách tìm nguyên hàm bằng phương pháp từng phần
Phương pháp giải & Ví dụ
Với bài toán tìm nguyên hàm của các hàm số dạng tích (hoặc thương) của hai hàm số “khác lớp hàm” ta thường sử dụng phương pháp nguyên hàm từng phần theo công thức
Dưới đây là một số trường hợp thường gặp như thế (với P(x) là một đa thức theo ẩn x)

Ví dụ minh họa
Bài 1: Tìm họ nguyên hàm của hàm số
a) ∫xsinxdx
b) ∫ex sinx dx
Hướng dẫn:
a) Xét ∫xsinxdx
Theo công thức tính nguyên hàm từng phần, ta có
F(x) = ∫xsinxdx = -xcosx+∫cosxdx = -xcosx+sinx+C
b) Xét F(x) = ∫ex sinx dx
F(x) = ex sinx-∫ex cosx dx = ex sinx-G(x) (1)
Với G(x) = ∫ex cosx dx
G(x) = ex cosx+∫ex sinx dx+C'=ex cosx+F(x)+C' (2)
Từ (1) và (2) ta có F(x) = ex sinx-ex cosx - F(x) - C'
Ghi nhớ: Gặp ∫emx+n.sin(ax+b)dx hoặc ∫emx+n.cos(ax+b)dx ta luôn thực hiện phương pháp nguyên hàm từng phần 2 lần liên tiếp.
Bài 2: Tìm họ nguyên hàm của hàm số
a) ∫x.2x dx
b) ∫(x2-1) ex dx
Hướng dẫn:
a) Xét ∫x.2x dx
b)
Suy ra ∫f(x)dx = (x2-1) ex - ∫2x.ex dx
Suy ra ∫f(x)dx = (x2-1) ex - ∫2x.ex dx = (x2-1) ex-(2x.ex - ∫2.ex dx)
= (x2-1) ex - 2x.ex + 2.ex+C = (x-1)2 ex + C.
Bài 3: Tìm họ nguyên hàm của hàm số
a) ∫2xln(x-1)dx
b)
Hướng dẫn:
a) Xét ∫2xln(x-1)dx
b)