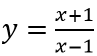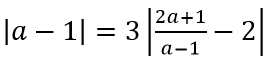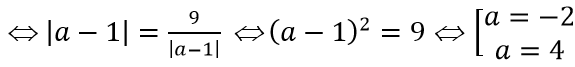Cách giải bài tập về tiệm cận của hàm số chi tiết
Với cách giải bài tập về tiệm cận của hàm số Toán lớp 12 với đầy đủ lý thuyết, phương pháp giải và bài tập có lời giải chi tiết giúp học sinh biết cách giải bài tập về tiệm cận của hàm số.
Cách giải bài tập về tiệm cận của hàm số cực hay
A. Phương pháp giải & Ví dụ

Ví dụ minh họa
Ví dụ 1: Tìm m để đồ thị hàm số 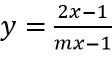
Hướng dẫn
Nghiệm của tử thức 2x - 1 = 0 ⇔ x = 1/2.
Để đồ thị hàm số có tiệm cận thì x = 1/2 không là nghiệm của mẫu hay m.1/2 - 1 ≠ 0 ⇔ m ≠ 2
Đường tiệm cận ngang y = 2/m
Phương trình hoành độ giao điểm của đường tiệm cận ngang y = 2/m và đường thẳng d:y = x là:
2/m = x
Mà hai đường này cắt nhau tại điểm A(1; 1) nên ta có 2/m = 1 ⇔ m = 2 (loại)
Vậy không tồn tại giá trị của m thỏa mãn yêu cầu bài toán.
Ví dụ 2: Tìm trên đồ thị hàm số 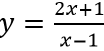
Hướng dẫn
Gọi M(a;(2a + 1)/(a - 1)) với a ≠ 1 là điểm thuộc đồ thị.
Đường tiệm cận đứng d1: x = 1; đường tiệm cận ngang d2:y = 2
Vì M cách đều hai tiệm cận của đồ thị hàm số nên
Với a = -2 thì tọa độ điểm M là M =(-2; 1)
Với a = 4 thì tọa độ điểm M là M =(4; 3)
Vậy các điểm cần tìm là M(-2; 1) và M(4; 3)
Ví dụ 3: Cho hàm số 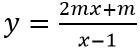
Hướng dẫn
Để x = 1 là tiệm cận đứng của đồ thị hàm số thì x = 1 là nghiệm của mẫu nhưng không là nghiệm của tử hay 2m.1 + m ≠ 0 ⇔ 3m ≠ 0 ⇔ m ≠ 0.
Đường tiệm cận đứng x = 1; đường tiệm cận ngang y = 2m
Vì đường tiệm cận đứng, tiệm cận ngang của đồ thị hàm số cùng hai trục tọa độ tạo thành một hình chữ nhật có diện tích bằng 8 nên
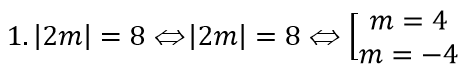
Giá trị của tham số m cần tìm là m = 4; m = -4.
B. Bài tập vận dụng
Câu 1: Tìm giá trị của tham số m để tiệm cận đứng của đồ thị hàm số 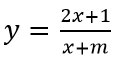
Câu 2: Cho hàm số 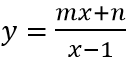
Câu 3: Cho hàm số 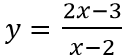
Câu 4: Cho hàm số 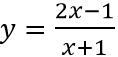
Câu 5:Cho hàm số 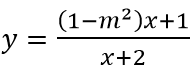
Câu 6: Cho hàm số 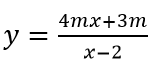
Câu 7: Cho hàm số 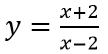
Câu 8: Cho hàm số