Khối đa diện lồi và khối đa diện đều chi tiết
Với Khối đa diện lồi và khối đa diện đều Toán lớp 12 với đầy đủ lý thuyết, phương pháp giải và bài tập có lời giải chi tiết giúp học sinh biết Khối đa diện lồi và khối đa diện đều.
Khối đa diện lồi và khối đa diện đều
Phương pháp giải & Ví dụ
1. Khối đa diện lồi là khối đa diện mà nếu đoạn thẳng nối bất kì hai điểm của nó thì luôn nằm trong nó.

2. Một khối đa diện đều là khối đa diện lồi thỏa mãn các tính chất sau đây:
+ Tất cả các mặt của nó là các đa giác đều, bằng nhau.
+ Mỗi đỉnh là giao của một số mặt bằng nhau (cũng là giao của số cạnh như nhau).
3. Khối đa diện đều loại {p; q} là khối đa diện mà mỗi mặt của nó là một đa giác đều p cạnh và mỗi đỉnh của nó là đỉnh chung của đúng q mặt
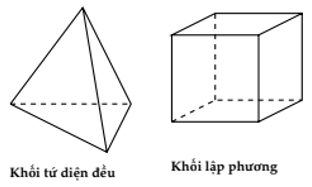
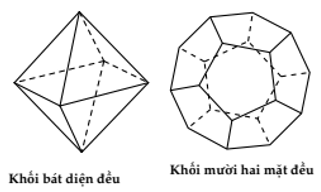
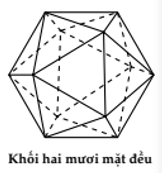
4. Định lí: Có đúng năm loại khối đa diện đều là:
Loại {3; 3}: Khối tứ diện đều
Loại {4; 3}: Khối lập phương
Loại {3; 4}: Khối bát diện đều
Loại {5; 3}: Khối 12 mặt đều
Loại {3; 5}: Khối 20 mặt đều.
| Khối đa diện đều | Loại | Số đỉnh | Số cạnh | Số mặt | Tâm đối xứng | Mặt đối xứng |
| Tứ diện đều | {3; 3} | 4 | 6 | 4 | 0 | 6 |
| Lập phương | {4; 3} | 8 | 12 | 6 | 1 | 9 |
| Bát diện đều | {3; 4} | 6 | 12 | 8 | 1 | 9 |
| Mười hai mặt đều | {5; 3} | 20 | 30 | 12 | 1 | 15 |
| Hai mươi mặt đều | {3; 5} | 12 | 30 | 20 | 1 | 15 |
Công thức tính: pM = 2C = qD hoặc công thức Euler: D – C + M = 2.