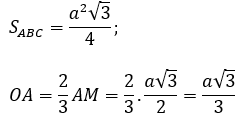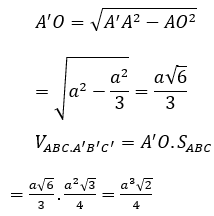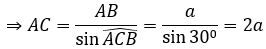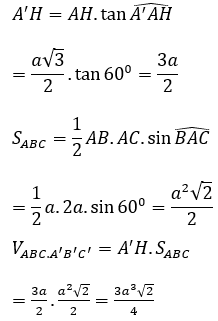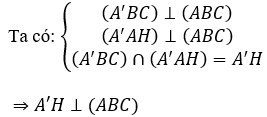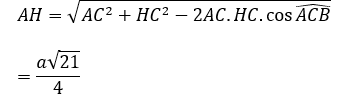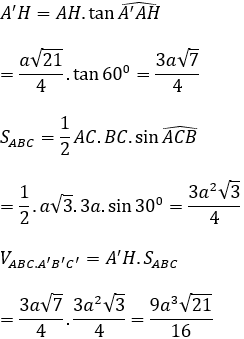Cách tính thể tích khối lăng trụ xiên chi tiết
Với Cách tính thể tích khối lăng trụ xiên Toán lớp 12 với đầy đủ lý thuyết, phương pháp giải và bài tập có lời giải chi tiết giúp học sinh biết Cách tính thể tích khối lăng trụ xiên.
Cách tính thể tích khối lăng trụ xiên
Phương pháp giải & Ví dụ
Hình lăng trụ xiên là hình lăng trụ có cạnh bên không vuông góc với đáy.

Ví dụ minh họa
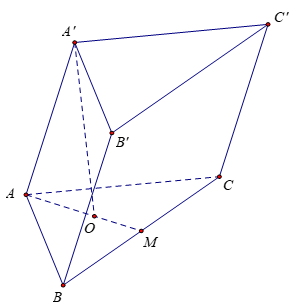
Bài 1: Cho hình lăng trụ ABC.A’B’C’, ∆ABC đều có cạnh bằng a, AA’ = a và đỉnh A’ cách đều A, B, C. Tính thể tích khối lăng trụ ABC.A’B’C’
Hướng dẫn:
Gọi M là trung điểm của AB, O là tâm của tam giác đều ABC.
Do A’ cách đều các điểm A, B, C nên A'O ⊥ (ABC)
Tam giác ABC đều cạnh a nên:
Xét ∆A’AO vuông tại O có:
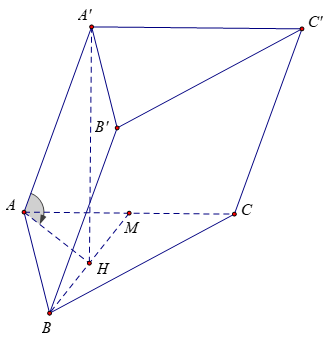
Bài 2: Cho hình lăng trụ ABC.A’B’C’ có đáy ABC là tam giác vuông tại B, AB = a, ∠(ACB) =300; M là trung điểm cạnh AC. Góc giữa cạnh bên và mặt đáy của lăng trụ bằng 600. Hình chiếu vuông góc của đỉnh A’ lên mặt phẳng (ABC) là trung điểm H của BM. Tính thể tích khối lăng trụ ABC.A’B’C’
Hướng dẫn:
A'H ⊥ (ABC) nên A’H là đường cao của lăng trụ
AH là hình chiếu vuông góc của AA’ lên mặt (ABC) nên góc giữa AA’ và (ABC) là góc (A'AH)=600
∆ABC vuông tại B có AB = a, ∠(ACB)=300
BM là trung tuyến
⇒BM=AM=AC/2=a
⇒BM=AM=AB=a
Do đó ∆ABM đều cạnh a có AH ⊥ BM
⇒AH=(a√3)/2
Xét tam giác AA’H có:
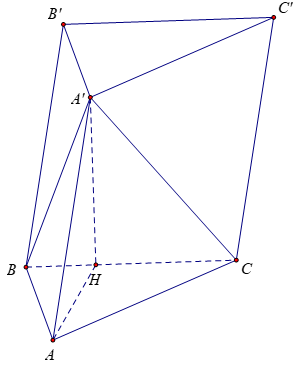
Bài 3: Cho hình lăng trụ ABC.A’B’C’, đáy ABC có AC = a√3, BC = 3a, ∠(ACB)=300. Cạnh bên hợp với mặt phẳng đáy góc 600 và mặt phẳng (A’BC) vuông góc với mặt phẳng (ABC). Điểm H trên cạnh BC sao cho HC = 3BH và mặt phẳng (A’AH) vuông góc với mặt phẳng (ABC). Tính thể tích khối lăng trụ ABC.A’B’C’
Hướng dẫn:
⇒AH là hình chiếu vuông góc của AA’ lên (ABCD)
Khi đó góc giữa AA’ và (ABCD) là góc (A'AH) =600
Ta có: BC = 3a, HC = 3BH ⇒ HC=9a/4
Xét tam giác ACH có:
Xét tam giác AA’H có: