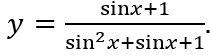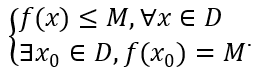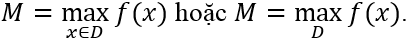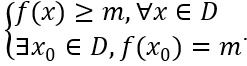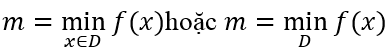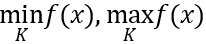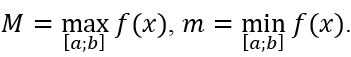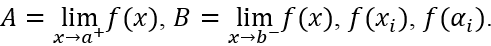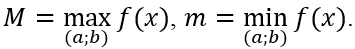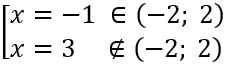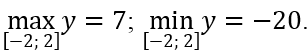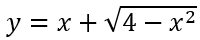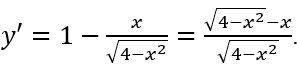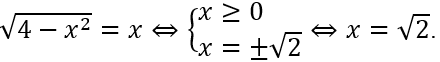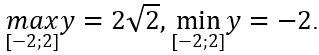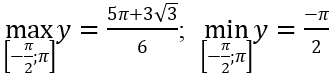Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số cực hay

A. Phương pháp giải & Ví dụ

1. Định nghĩa: Cho hàm số y = f(x) xác định trên miền D

Số M gọi là giá trị lớn nhất của hàm số y = f(x) trên D nếu: 

Kí hiệu: 

Số m gọi là giá trị nhỏ nhất của hàm số y = f(x) trên D nếu: 

Kí hiệu: 

2. Quy trình tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số sử dụng bảng biến thiên

Bước 1. Tính đạo hàm f'(x).

Bước 2. Tìm các nghiệm của f'(x) và các điểm f'(x)trên K.

Bước 3. Lập bảng biến thiên của f(x) trên K.

Bước 4. Căn cứ vào bảng biến thiên kết luận 

3. Quy trình tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số không sử dụng bảng biến thiên

Trường hợp 1. Tập K là đoạn [a; b]

Bước 1. Tính đạo hàm f'(x).

Bước 2. Tìm tất cả các nghiệm x_i ∈[a; b] của phương trình f'(x) = 0 và tất cả các điểm α_i ∈ [a; b] làm cho f'(x) không xác định.

Bước 3.Tính f(a), f(b), f(x_i), f(α_i).

Bước 4. So sánh các giá trị tính được và kết luận 

Trường hợp 2. Tập K là khoảng (a; b)

Bước 1. Tính đạo hàm f'(x).

Bước 2. Tìm tất cả các nghiệm x_i ∈ (a; b) của phương trình f'(x) = 0 và tất cả các điểm α_i ∈ (a; b) làm cho f'(x) không xác định.

Bước 3. Tính 

Bước 4. So sánh các giá trị tính được và kết luận 

Chú ý: Nếu giá trị lớn nhất (nhỏ nhất) là A hoặc B thì ta kết luận không có giá trị lớn nhất (nhỏ nhất).

Ví dụ minh họa

Ví dụ 1: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = x³ - 3x² - 9x + 2 trên đoạn [-2; 2].

Hướng dẫn

Ta có: y' = 3x² - 6x - 9 = 0 ⇔

Mà y(-2) = 0; y(2) = -20; y(-1) = 7.

Suy ra 

Ví dụ 2: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số 

Hướng dẫn

Tập xác định: D = [-2; 2]. Ta có: 

Khi đó y' = 0 ⇔ 

Có y(√2) = 2√2, y(2) = 2 ,y(-2) = -2.

Vậy 

Ví dụ 3: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = x - sin⁡2x trên đoạn [π/2; π]

Hướng dẫn

Ta có y' = 1 - 2cos2x = 0 ⇔ cos2x = 1/2 = cos π/3 ⇔ x = ±π/6 + kπ.

Xét x ∈[(-π)/2; π] ta được x = ±π/6; x = 5π/6.

f((-π)/2) = -π/2; f(π) = π; f((-π)/6) = -π/6 + √3/2; f(π/6) = π/6 - √3/2; f(5π/6) = 5π/6 + √3/2.

Suy ra 

B. Bài tập vận dụng

Câu 1: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số f(x) = x³ - 3x² - 9x + 35 trên đoạn [-4; 4]

Câu 2: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số 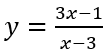 trên [0; 2]

Câu 3: Gọi m là giá trị nhỏ nhất của hàm số 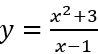 trên đoạn [2; 4]. Tìm m.

Câu 4: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số 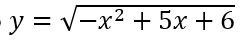 trên đoạn [-1; 6]

Câu 5: Tìm tổng giá trị lớn nhất và nhỏ nhất của hàm số y = f(x) = |x| + 3 trên [-1; 1]

Câu 6: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số 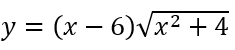trên đoạn [0; 3]

Câu 7: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = 2sin² x + 2sinx - 1 bằng

Câu 8: Cho hàm số  Gọi M là giá trị lớn nhất và m là giá trị nhỏ nhất của hàm số đã cho. Tìm M và m.