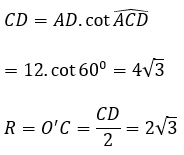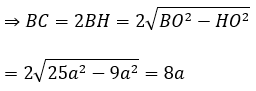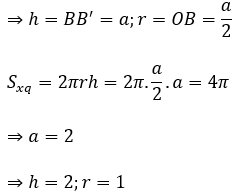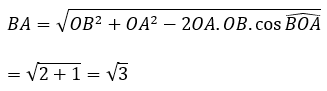Cách xác định thiết diện của hình trụ

Phương pháp giải & Ví dụ

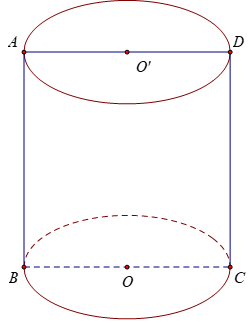
- Nếu cắt mặt trụ tròn xoay (có bán kính là r) bởi một mặt phẳng (α) vuông góc với trục Δ thì ta được đường tròn có tâm trên Δ và có bán kính bằng r với r cũng chính là bán kính của mặt trụ đó.

- Nếu cắt mặt trụ tròn xoay (có bán kính là r) bởi một mặt phẳng (α) không vuông góc với trục Δ nhưng cắt tất cả các đường sinh, ta được giao tuyến là một đường elíp có trụ nhỏ bằng 2r và trục lớn bằng 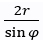, trong đó φ là góc giữa trục Δ và mặt phẳng (α) với 0 < φ < 90º.

- Cho mặt phẳng (α) song song với trục Δ của mặt trụ tròn xoay và cách Δ một khoảng k.

    + Nếu k < r thì mặt phẳng (α) cắt mặt trụ theo hai đường sinh thì thiết diện là hình chữ nhật.

    + Nếu k = r thì mặt phẳng (α) tiếp xúc với mặt trụ theo một đường sinh.

    + Nếu k > r thì mặt phẳng (α) không cắt mặt trụ.

Ví dụ minh họa

Bài 1: Khối trụ có thiết diện qua trục là hình vuông cạnh 2a, tính diện tích xung quanh, diện tích toàn phần và thể tích của khối trụ

Hướng dẫn:

Thiết diện là hình vuông ABCD cạnh 2a

Đường cao của hình trụ là AB = 2a, bán kính đáy OB = a.

Diện tích xung quanh của khối trụ là: S_xq = 2πrh=2π.a.2a=4πa²

Diện tích toàn phần của khối trụ là S_tp = 2πrh+2πr²=4πa²+2πa²=6πa²

Thể tích của khối trụ là: V=πr² h=π.a².2a=2πa³

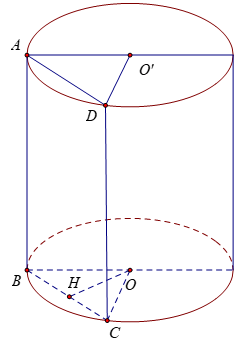
Bài 2: Khối trụ có bán kính đáy R = a .Thiết diện song song với trục và cách trục khối trụ một khoảng bằng a/2 là hình chữ nhật có diện tích bằng a² √3 .Tính thể tích khối trụ

Hướng dẫn:

∆BOC cân tại O có OH là đường cao

⇒ H là trung điểm của BC

ABCD là hình chữ nhật nên:

S_ABCD = AB.BC=AB.a√3=a² √3⇒ AB=a

Thể tích của khối trụ là:

V=πr² h=π.a².a= πa³

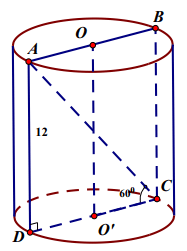
Bài 3: Cắt khối trụ bởi một mặt phẳng qua trục ta được thiết diện là hình chữ nhật ABCD có AB và CD thuộc hai đáy của khối trụ. Biết AD = 12 cm và góc ACD bằng 60º. Tính thể tích của khối trụ

Hướng dẫn:

Xét tam giác ADC vuông tại C có:

Thể tích của khối trụ là:

V=πr² h=π.(2√3)².12=144π

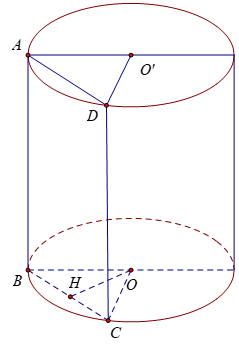
Bài 4: Một hình trụ có bán kính đáy r = 5a và khoảng cách giữa hai đáy bằng 7a. Cắt khối trụ bởi một mặt phẳng song song với trục và cách trục 3a. Tính diện tích của thiết diện.

Hướng dẫn:

Thiết diện tạo thành là hình chữ nhật ABCD có AB = 7a

Từ O kẻ OH vuông góc với BC

⇒ OH=3a

∆BOC cân tại O có OH là đường cao

⇒ H là trung điểm của BC

Diện tích của thiết diện là:

S_ABCD = AB.BC=7a.8a = 56a²

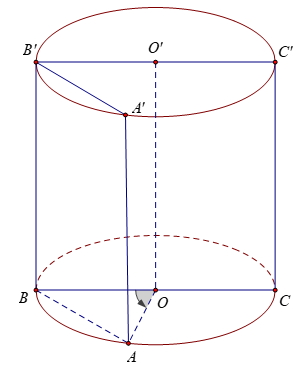
Bài 5: Một hình trụ có diện tích xung quanh là 4π, thiết diện qua trục là một hình vuông. Một mp (P) song song với trục, cắt hình trụ theo thiết diện ABB’A’, biết một cạnh của thiết diện là một dây của đường tròn đáy hình trụ và căng một cung 120º. Tính diện tích thiết diện ABB’A’ .

Hướng dẫn:

Gọi h, r là chiều cao và bán kính đáy của trụ.

Thiết diện qua trục là hình vuông BCC’B’ cạnh a

Dây AB căng cung 120º nên ∠(BOA) = 120º

Xét tam giác BOA có :

Diện tích thiết diện BAA’B’ là :

S=AB.BB'=2√3