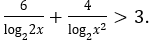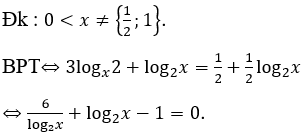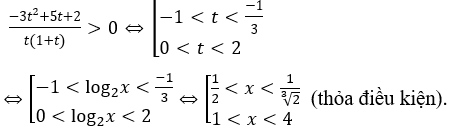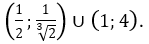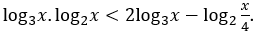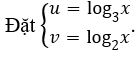Cách Giải bất phương trình logarit bằng cách đặt ẩn phụ chi tiết
Với cách Giải bất phương trình logarit bằng cách đặt ẩn phụ của hàm số Toán lớp 12 với đầy đủ lý thuyết, phương pháp giải và bài tập có lời giải chi tiết giúp học sinh biết cách Giải bất phương trình logarit bằng cách đặt ẩn phụ .
Giải bất phương trình logarit bằng cách đặt ẩn phụ
Phương pháp giải & Ví dụ
Mục đích chính của phương pháp này là chuyển các bài toán đã cho về bất phương trình đại số quen thuộc, đặc biệt là các bất phương trình bậc hai hoặc hệ bất phương trình.

Ví dụ minh họa
Bài 1: Giải bất phương trình sau log52 x+4log25x-8 < 0.
Hướng dẫn:
Đk: x > 0.
BPT ⇔ log52x + 2log5x - 8 < 0.
Đặt t = log5x. Khi đó bất phương trình trở thành.
t2+2t-8 < 0 ⇔ -4 < t < 2 ⇔ -4 < log5x < 2 ⇔ 5-4 < x < 25 (thỏa điều kiện).
Vậy tập nghiệm của bất phương trình là : (5-4; 25).
Bài 2: Giải bất phương trình sau
Hướng dẫn:
Đặt t=log2x ≠ 0. Khi đó bất phương trình trở thành.
Vậy tập nghiệm của bất phương trình là:
Bài 3: Giải bất phương trình sau
Hướng dẫn:
Đk : x > 0.
Viết lại bất phương trình dưới dạng log3x.log2x-2log3x-log2x-2 < 0.
Khi đó bất phương trình trở thành.
uv-2u-v-2 < 0 ⇔ (u-1)(v-2) < 0.
Vậy tập nghiệm của bất phương trình là: (3;4).