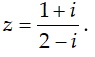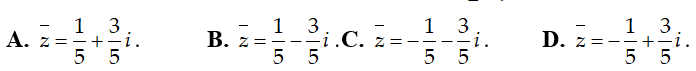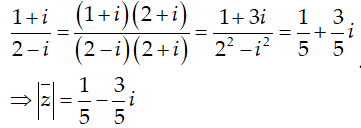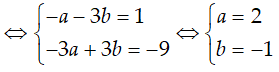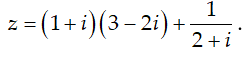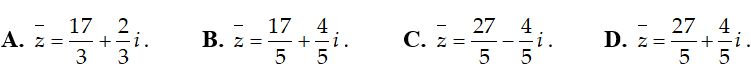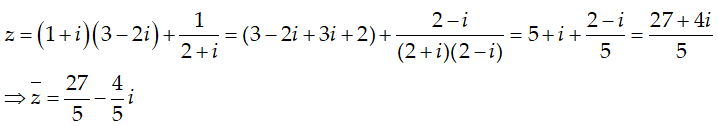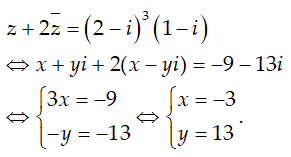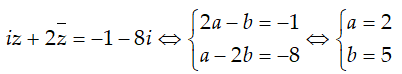Cách tìm số phức liên hợp cực hay, chi tiết

Phương pháp giải

Cho số phức z = a + bi. Ta gọi số phức liên hợp của z là  = a - bi.

Kết quả: ∀ z ∈ C ta có:

Z là số thực khi z = 

Z là số thuần ảo khi z = -

Ví dụ minh họa

Ví dụ 1: Cho số phức z = 1 + 3i Tìm số phức 

A.  = 1 - 3i.        B.  = 3 - i.        C.  = 3 + i.         D. = 1 + 3i.

Hướng dẫn:

Với z = 1 + 3i thì  = 1 - 3i

Chọn A.

Ví dụ 2: Cho số phức z = -2 - 5i Tìm phần thực a và phần ảo b của số phức  .

A. a = -2 ; b = 5         B. a = -2; b = -5         C. a = -5; b = 2         D. a = -5; b = -2

Hướng dẫn:

z = a + bi =>  = a - bi

Nên  = -2 + 5i vậy. Phần thực bằng a = -2 và phần ảo b = 5

Chọn A.

Ví dụ 3:Tìm số phức liên hợp của số phức 

Hướng dẫn:

Chọn B.

Ví dụ 4:Tìm số phức z thỏa mãn z - (2 + 3i) = 1 - 9i .

A. z = -3 - i.         B. z = -2 - i.         C. z = 2 - i         . D. z = 2 + i.

Hướng dẫn:

Gọi z = a + bi

z - (2 + 3i) = 1 - 9i <=> a + bi - 2a + 2bi - 3ai - 3b = i - 9i

Vậy z = 2 - i

Chọn C.

Ví dụ 5:Cho số phức z = 3 + 4i. Tìm phần thực a và phần ảo b của số phức  .

A. a = 3; b = 4         B. a = 3; b = -4         C. a = 4; b = 3         D. a = 4; b = -3

Hướng dẫn:

z = a + bi =>  = a - bi

vậy  = 3 - 4i

= >Phần thực a = 3 và phần ảo bằng b = -4

Chọn B.

Ví dụ 6:Cho số phức  = 4 - 3i . Tìm phần thực và phần ảo của số phức z.

A. a = 3 ; b = 4        B. a = 3; b = -4        C. a = 4; b = 3        D. a = 4; b = -3

Hướng dẫn:

z = a + bi =>  = a - bi

vậy z = 4 + 3i

=> Phần thực a = 4 và phần ảo b = 3

Chọn C.

Ví dụ 7:Tìm số phức liên hợp của số phức 

Hướng dẫn:

Chọn C.

Ví dụ 8:Tìm phần ảo b của số phức z thỏa mãn z + 2 = (2 - i)²(1 - i)

A. b = 13        B.b = -13        C. b = -9        D. b = 9

Hướng dẫn:

Đặt z = x + yi

Chọn A.

Ví dụ 9:Tìm số phức iz + 2 = -1 - 8i thỏa mãn .

A. z = 7 + 7i         B. z = 5 - 2i.         C. z = 2 + 5i.         D. z = 1 - 2i.

Hướng dẫn:

Gọi z = a + bi khi đó  = a - bi

Ta có:

Vậy z = 2 + 5i