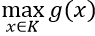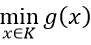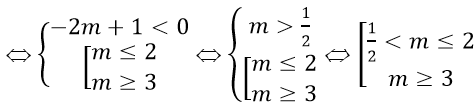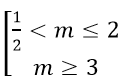Phương pháp cô lập m trong khảo sát tính đơn điệu của hàm số cực hay

A. Phương pháp giải & Ví dụ

Phương pháp giải

Bước 1: Tìm y'

Hàm số đồng biến trên khoảng K khi và chỉ khi y' ≥ 0 ∀ x ∈ K

Hàm số nghịch biến trên khoảng K khi và chỉ khi y' ≤ 0 ∀x ∈ K

Bước 2: Cô lập tham số m đưa về dạng m≥g(x) hoặc m ≤ g(x)

Bước 3: Vẽ bảng biến thiên của g(x)

Bước 4: Kết luận

m ≥ g(x) ∀ x ∈ K khi và chỉ khi m ≥ 

m ≤ g(x) ∀ x ∈ K khi và chỉ khi m ≤ 

Một số hàm số thường gặp

Hàm đa thức bậc ba: y = f(x) = ax³ + bx² + cx + d (a ≠ 0)

⇒ f'(x) = 3ax² + 2bx + c

Với a > 0 và f'(x) có hai nghiệm phân biệt x₁ < x₂

Hàm số đồng biến trên (α; β) khi và chỉ khi β ≤ xc hoặc α ≥ x₂

Hàm số nghịch biến trên (α; β) khi và chỉ khi x₁ ≤ α < β ≤ x₂

Với a <0 và f'(x) có hai nghiệm phân biệt x₁ < x₂

Hàm số đồng biến trên (α; β) khi và chỉ khi x₁ ≤ α < β ≤ x₂

Hàm số nghịch biến trên (α; β) khi và chỉ khi β≤x₁ hoặc α ≥ x₂

Hàm phân thức bậc nhất: y = (ax + b)/(cx + d) ⇒ y'= (ad - bc)/(cx + d)²

Hàm số đồng biến trên khoảng K khi và chỉ khi ad-bc>0 và -d/c ∉ K

Hàm số nghịch biến trên khoảng K khi và chỉ khi ad - bc < 0 và -d/c ∉ K

Ví dụ minh họa

Ví dụ 1: Tìm m để hàm số y = x³/3 - mx²+(1 - 2m)x- 1 đồng biến trên (1; +∞)

Hướng dẫn

TXĐ: D = R

Ta có y' = x² - 2mx + 1 - 2m

Hàm số đã cho đồng biến trên (1; +∞)⇔ ∀ x ∈(1; +∞),y' ≥ 0

⇔ ∀ x ∈ (1; +∞), x² -2mx + 1 - 2m ≥ 0 ⇔ ∀ x ∈(1; +∞), x² + 1 ≥ 2m(x + 1)

⇔ ∀ x ∈(1; +∞),2m ≤ (x² + 1)/(x + 1) (do x + 1 > 0 khi x > 1)

Xét hàm số f(x) = (x² + 1)/(x + 1), x ∈ (1; +∞)

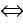
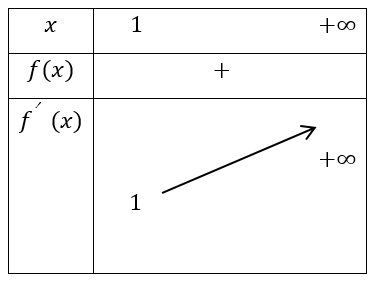
f'(x) = (x² + 2x - 1)/(x + 1)² >0 với mọi x  (1;+∞)

Ta có bảng biến thiên:

Dựa vào bảng biến thiên để 2m ≤ f(x),∀ x ∈(1; +∞) thì 2m ≤ 1 ⇔ m ≤ 1/2

Ví dụ 2: Tìm giá trị của tham số m để hàm số y = (2x - 1)/(x - m) nghịch biến trên khoảng (2; 3)

Hướng dẫn

TXĐ: D=R\{m}.

Ta có y'= (-2m + 1)/(x - m)² . Để hàm số nghịch biến trên khoảng (2; 3) thì hàm só phải xác định trên khoảng (2; 3) và y' < 0 ∀ x ∈ (2; 3).

Vậy giá trị của tham số m cần tìm là 

Ví dụ 3: Tìm các giá trị m để hàm số y = mx³ - x² + 3x + m - 2 đồng biến trên (-3 ; 0)

Hướng dẫn

TXĐ: D = R

Ta có y'= 3mx² - 2x + 3. Hàm số đồng biến trên khoảng (-3; 0) khi và chỉ khi:

y' ≥ 0,∀ x ∈(-3; 0) (Dấu '' = '' xảy ra tại hữu hạn điểm trên (-3; 0))

⇔ 3mx² - 2x + 3 ≥ 0, ∀ x ∈(-3; 0)

⇔ m ≥(2x-3)/(3x² ) = g(x) ∀ x ∈(-3;0)

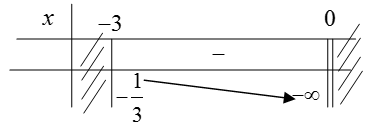
Ta có: g'(x) = (-2x + 6)/(3x³ ); g'(x) = 0 ⇔ x = 3

Bảng biến thiên

Vậy m ≥ 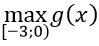= -1/3.

B. Bài tập vận dụng

Câu 1: Tìm tất cả giá trị của tham số m để hàm số y = mx² - (m + 6)x nghịch biến trên khoảng (-1; +∞)

Câu 2: Cho hàm số y = x³-3mx²+3(m² - 1)x - 2m + 3. Tìm m để hàm số nghịch biến trên khoảng (1; 2).

Câu 3: Tất cả các giá trị thực của tham số m sao cho hàm số y = -x⁴ + (2m - 3)x² + m nghịch biến trên khoảng (1; 2) là (-∞; p/q], trong đó phân số p/q tối giản và q > 0. Tính tổng p+q

Câu 4: Tìm tất cả các giá trị thực của tham số m sao cho hàm số 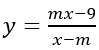 đồng biến trên khoảng (2; +∞).

Câu 5: Tìm giá trị của m để hàm số 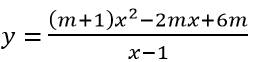 đồng biến trên khoảng (4; +∞)

Câu 6: Tìm tất cả các giá trị thực của tham số m để hàm số 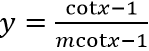 đồng biến trên khoảng (π/4; π/2).

Câu 7: Tìm m để hàm số 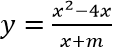 đồng biến trên [1; +∞).

Câu 8: Với giá trị nào của m thì hàm số y=√(x²+2mx+m²+1) đồng biến trên khoảng (1; +∞).