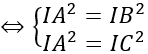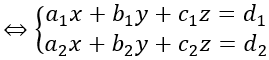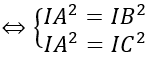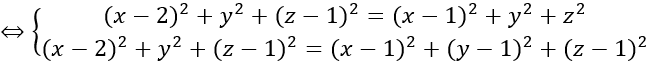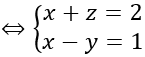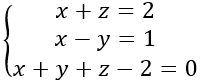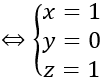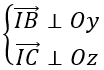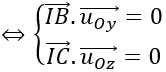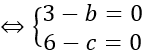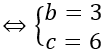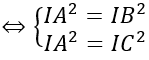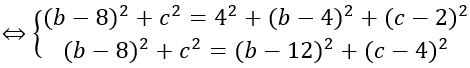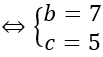Viết phương trình mặt cầu đi qua 3 điểm chi tiết
Với Viết phương trình mặt cầu đi qua 3 điểm Toán lớp 12 với đầy đủ lý thuyết, phương pháp giải và bài tập có lời giải chi tiết giúp học sinh biết Viết phương trình mặt cầu đi qua 3 điểm .
Viết phương trình mặt cầu đi qua 3 điểm
Phương pháp giải
Gọi I (x; y; z ) là tâm mặt cầu đi qua 3 điểm A, B, C
⇔ IA=IB=IC
+ Dựa vào điều kiện cho trước để tìm phương trình còn lại
⇒ Tọa độ tâm I, R2 =IA2
⇒ Phương trình mặt cầu cần tìm.

Ví dụ minh họa
Bài 1: Cho 3 điểm A ( 2; 0; 1), B (1; 0; 0), C (1; 1; 1) và mặt phẳng (P): x + y + z – 2 = 0. Viết phương trình mặt cầu đi qua 3 điểm A, B, C và có tâm thuộc mặt phẳng (P)
Hướng dẫn:
Gọi I (x; y; z) là tâm mặt cầu đi qua 3 điểm A, B, C
⇔ IA=IB=IC
Do tâm của mặt cầu thuộc mặt phẳng (P) nên: x + y + z – 2 = 0
Ta có hệ phương trình
Vậy I (1; 0; 1) và R2 =IA2=1
Vậy phương trình mặt cầu cần tìm là:
(x-1)2 +y2 +(z-1)2 =1
Bài 2: : Trong không gian hệ tọa độ Oxyz, cho 3 điểm A (1; 0; 0), B (0; 3; 0), C (0; 0; 6). Tìm phương trình mặt cầu (S) tiếp xúc với Oy tại B, tiếp xúc với Oz tại C và đi qua A
Hướng dẫn:
Gọi I (a; b; c) là tâm mặt cầu
IB→=(-a;3-b; -c); IC→=(-a; -b;6-c)
Do mặt cầu (S) tiếp xúc với Oy tại B, tiếp xúc với Oz tại C nên
⇒ I(a;3;6)
I đi qua A nên ta có IA = IB
⇔ IA2 =IB2 ⇔ (a-1)2 +32 +62 =a2 +62
⇔ a=5
Khi đó, I (5; 3; 6) và R2=IA2 =61
Vậy phương trình mặt cầu cần tìm là :
(x-5)2 +(y-3)2 +(z-6)2 =61
Bài 3:Viết phương trình mặt cầu (S) đi qua A (0; 8; 0), B (4; 6; 2), C (0; 12; 4) và có tâm I thuộc mặt phẳng (Oyz)
Hướng dẫn:
Do tâm I thuộc mặt phẳng (Oyz) nên I (0; b; c)
Mặt cầu đi qua A, B, C nên IA = IB = IC
Vậy I (0; 7; 5); R2 =IA2 =26
Vậy phương trình mặt cầu cần tìm là
x2 +(y-7)2 +(z-5)2 =26