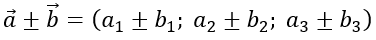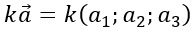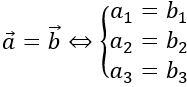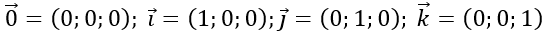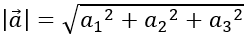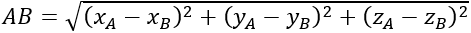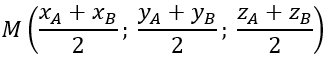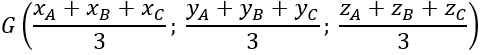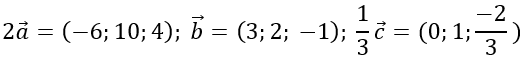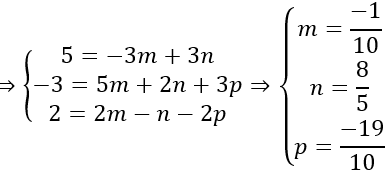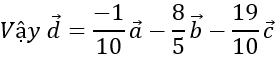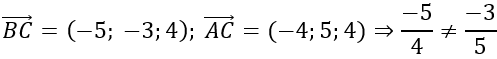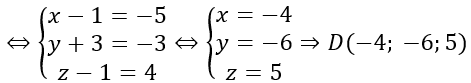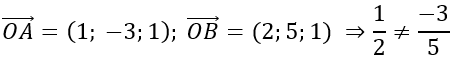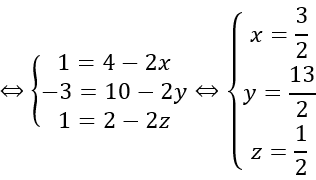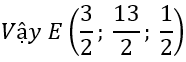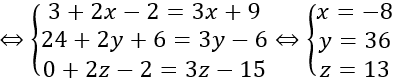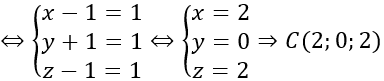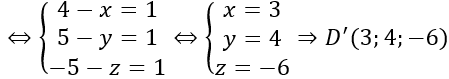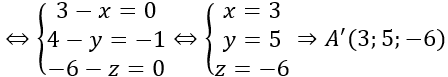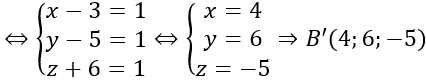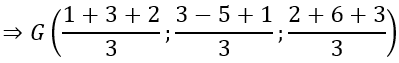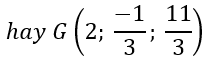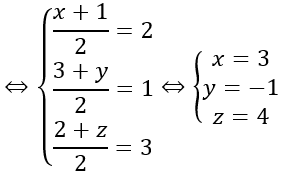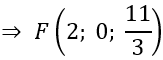Tìm tọa độ của vecto, của điểm

Phương pháp giải & Ví dụ

1. Tọa độ của vecto

a) Định nghĩa

Ta gọi bộ ba số (x; y; z) là tọa độ của vecto u→ đối với hệ tọa độ Oxyz cho trước

     u→=(x;y;z)⇔u→=xi→+yj→+zk→

b) Tính chất

Trong không gian Oxyz, cho hai vecto a→ =(a₁;a₂;a₃ ) và b→ =(b₁;b₂;b₃ ); k∈R

+

+

+

+

+

+

2. Tọa độ của điểm

a) Định nghĩa

M(x;y;z)⇔OM→= xi→+yj→+zk→(x: hoành độ, y: tung độ, z: cao độ)

b) Tính chất

Cho A(x _A; y _A; z _A );B(x _B; y _B; z _B )

+ AB→ =(x_A-x_B;y_A-y_B;z_A-z_B )

+

+ Tọa độ trung điểm M của đoạn thẳng AB:

+

+ Tọa độ trọng tâm G của tam giác ABC:

+

+ Tọa độ trọng tâm G của tứ diện ABCD:

+

Ví dụ minh họa

Bài 1:Trong hệ trục tọa độ Oxyz, cho các vecto a→ =-3i→ +5j→ +2k→ ; b→ =(3;2; -1); c→ =3j→ -2k→ ; d→ =(5; -3;2)

a) Tìm tọa độ của các vecto a→ - 2b→ + c→ ; 3b→ -2c→ +d→

b) Tìm tọa độ của vecto 2a→ -b→ +1/3c→

c) Phân tích vecto d→ theo 3 vecto a→ ; b→ ; c→

Hướng dẫn:

a) a→ =(-3;5;2); 2b→ =(6;4; -2); c→ =(0;3; -2)

⇒ a→- 2 b→+ c→=(-9;4; 2)

3 b→=(9;6; -3); 2 c→=(0;6; -4); d→=(5; -3;2)

⇒3 b→-2 c→+ d→=(14; -3;7)

b)

c) giả sử d→=ma→+nb→+pc→

Bài 2:Trong không gian với hệ trục tọa độ Oxyz, cho các điểm A(1; -3;1);B(2;5;1) và vecto OC→=-3 i→+2 j→+5 k→

a) Tìm tọa độ điểm D sao cho ABCD là hình bình hành.

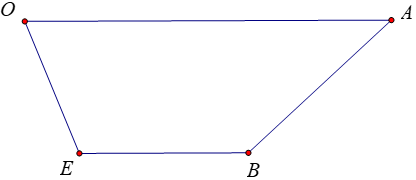
b) Tìm tọa độ điểm E sao cho tứ giác OABE là hình thang có hai đáy OA, BE và OA = 2BE.

c) Tìm tọa độ điểm M sao cho 3 AB→+2 AM→=3 CM→

Hướng dẫn:

a)

⇒BC→; AC→ không cùng phương hay A, B, C không thẳng hàng

Gọi D (x; y; z) ⇒AD→=(x-1;y+3;z-1)

ABCD là hình bình hành ⇔AD→=BC→

b)

Ta có:

⇒OA→; OB→ không cùng phương hay O, A, B không thẳng hàng.

Gọi E (x; y; z) ⇒EB→=(2-x;5-y;1-z)

Theo đề bài, tứ giác OABE là hình thang có hai đáy OA, BE và OA = 2BE.

⇒OA→=2EB→

c) Gọi M (x; y; z). Ta có:

AB→=(1;8;0)⇒3AB→=(3;24;0)

AM→=(x-1;y+3;z-1)⇒2AM→=(2x-2;2y+6;2z-2)

CM→=(x+3;y-2;z-5)⇒3CM→=(3x+9;3y-6;3z-15)

3AB→+2AM→=3CM→

Vậy M(-8; 36; 13)

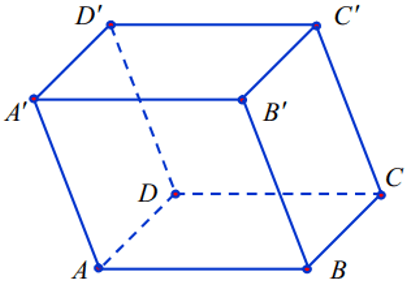
Bài 3:Trong không gian hệ trục tọa độ Oxyz, cho hình hộp ABCD.A’B’C’D’ biết A(1;0;1),B(2;1;2),D(1; -1;1);C^' (4;5; -5). Xác định tọa độ các đỉnh còn lại của hình hộp ABCD.A’B’C’D’.

Hướng dẫn:

+ Gọi C (x; y; z)

Ta có: AB→ =(1;1;1);DC→ =(x-1;y+1;z-1)

Tứ giác ABCD là hình bình hành ⇔AB→ =DC→

+ Gọi D’ (x; y; z)

Ta có: D^'C^'→ =(4-x;5-y; -5-z); DC→ =(1;1;1)

Tứ giác DCC’D’ là hình bình hành ⇔D^'C^'→=DC→

+ Gọi A’ (x; y; z)

Ta có: A^'D^'→=(3-x;4-y; -6-z); AD→=(0; -1;0)

Tứ giác ADD’A’ là hình bình hành ⇔A^'D^'→=AD→

+ Gọi B’ (x; y; z)

Ta có: D^'C^'→=(1;1;1);A^'B^'→=(x-3;y-5;z+6)

Tứ giác ABCD là hình bình hành ⇔A^'B^'→=D^'C^'→

Bài 4: Trong không gian với hệ trục tọa độ Oxyz, cho tam giác ABC có A(1; 3; 2), B(3; -5; 6), C (2; 1; 3).

a) Tìm tọa độ trung điểm M của cạnh AB

b) Tìm tọa độ trọng tâm G của tam giác ABC và hình chiếu của G lên Ox

c) Tìm tọa độ điểm N đối xứng với điểm A qua điểm C

d) Tìm tọa độ điểm F trên mặt phẳng Oxz sao cho |FA→+FB→+FC→ | nhỏ nhất

e) Tìm tọa độ điểm B’ đối xứng với điểm B qua trục tung.

Hướng dẫn:

a) M là trung điểm của cạnh AB

hay M(2; -1;4)

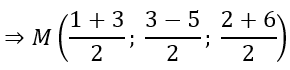
b) G là trọng tâm của tam giác ABC

Hình chiếu của G lên trục Ox là H (2; 0; 0)

c) Gọi N (x; y; z)

N đối xứng với A qua C ⇔ C là trung điểm của AN

⇒N(3; -1;4)

d) Ta có: |FA→ +FB→ +FC→ |=|3FG→ |=3FG

Do đó: |FA→ +FB→ +FC→ | nhỏ nhất ⇔ FG nhỏ nhất ⇔ F là hình chiếu của G lên mặt phẳng (Oxz)

e) Hình chiếu của B lên trục Oy là H (0; -5; 0)

B’ là điểm đối xứng với điểm B qua trục tung ⇔ H là trung điểm của đoạn BB’

⇒B'(-3; -5; -6)