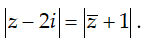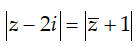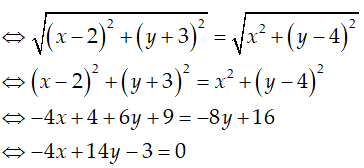Tập hợp điểm biểu diễn số phức là đường thẳng chi tiết
Với Tập hợp điểm biểu diễn số phức là đường thẳng Toán lớp 12 với đầy đủ lý thuyết, phương pháp giải và bài tập có lời giải chi tiết giúp học sinh biết Tập hợp điểm biểu diễn số phức là đường thẳng.
Tập hợp điểm biểu diễn số phức là đường thẳng
Ví dụ 1:Tập hợp điểm biểu diễn các số phức z thỏa mãn điều kiện |z - (1 + i)| = |z + 2i| là đường nào sau đây ?
A. Đường thẳng. B. Đường tròn. C. Elip. D. Parabol.
Hướng dẫn:
Gọi z = x + yi, (x;y ∈ R) được biểu diễn bởi điểm M(x;y) trong mặt phẳng Oxy.
Suy ra tập hợp điểm biểu diễn số phức z là đường thẳng x + 3y + 1 = 0.
Chọn A.

Ví dụ 2:Tìm tập hợp những điểm M biểu diễn số phức z trong mặt phẳng phức, biết số phức z thỏa mãn điều kiện
A. Tập hợp những điểm Mlà đường thẳng có phương trình 4x + 2y + 3 = 0.
B. Tập hợp những điểm M là đường thẳng có phương trình 4x - 2y + 3 = 0.
C. Tập hợp những điểm M là đường thẳng có phương trình 2x + 4y - 3 = 0.
D. Tập hợp những điểm M là đường thẳng có phương trình 2x + 4y + 3 = 0.
Hướng dẫn:
Gọi z = x + yi,(x;y ∈ R)
Ta có:
<=>|x + (y-2)i| = |(x+1) - yi|
<=> x2 + (y - 2)2 = (x + 1)2 + y2
<=> 2x + 4y - 3 = 0
Tập hợp những điểm M là đường thẳng có phương trình 2x + 4y - 3 = 0.
Chọn C.
Ví dụ 3:Tập hợp điểm biểu diễn các số phức z thỏa mãn điều kiện |z -2 + 3i| = |z-4i| là đường nào sau đây ?
A. Đường thẳng. B. Đường tròn. C. Elip. D. Parabol.
Hướng dẫn:
Gọi z = x + yi, được biểu diễn bởi điểm M(x;y) trong mặt phẳng Oxy.
Ta có: |z -2 + 3i| = |z - 4i| <=> |x + yi -2 + 3i| = |x + yi - 4i|
Suy ra tập hợp điểm biểu diễn số phức z là đường thẳng -4x + 14y -3 = 0.
Chọn A.