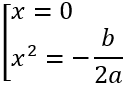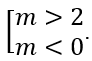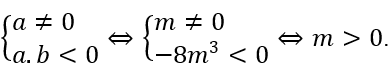Biện luận theo m số cực trị của hàm số cực hay

A. Phương pháp giải & Ví dụ

Phương pháp giải

1. Cực trị của hàm số bậc ba

Cho hàm số y = ax³ + bx² + cx + d, a ≠ 0.

y' = 0 ⇔ 3ax² + 2bx + c = 0 (1) ; Δ'_y' = b² - 3ac

    Phương trình (1) vô nghiệm hoặc có nghiệm kép thì hàm số đã cho không có cực trị.

    Hàm số bậc 3 không có cực trị ⇔ b² - 3ac ≤ 0

    Phương trình (1) có hai nghiệm phân biệt thì hàm số đã cho có 2 cực trị.

     Hàm số bậc 3 có 2 cực trị ⇔ b² - 3ac > 0

2. Cực trị của hàm số bậc bốn trùng phương

Cho hàm số: y = ax⁴ + bx² + c (a ≠ 0) có đồ thị là (C).

y' = 4ax³ + 2bx; y' = 0 ⇔ 

    (C)có một điểm cực trị y' = 0 có 1 nghiệm x = 0 ⇔ -b/2a ≤ 0 ⇔ ab ≥ 0.

    (C)có ba điểm cực trị y' = 0 có 3 nghiệm phân biệt ⇔ -b/2a > 0 ⇔ ab < 0.

Ví dụ minh họa

Ví dụ 1: Tìm m để hàm số y = x³ + mx + 2 có cả cực đại và cực tiểu.

Hướng dẫn

y' = 3x² + m.

Hàm số y = x³ + mx + 2 có cả cực đại và cực tiểu khi và chỉ khi y'= 0 có hai nghiệm phân biệt.

Vậy m < 0.

Ví dụ 2: Cho hàm số y = (m - 2)x³ - mx - 2. Với giá trị nào của m thì hàm số có cực trị?

Hướng dẫn

Tập xác định D = R.

Tính y' = 3(m - 2)x² - m.

Cho y' = 0 ⇔ 3(m - 2)x² - m = 0   (1).

   + TH1: Xét m = 2 ⇒ y' = -2 < 0 ∀ x nên hàm số đã cho không có cực trị.

   + TH2: Xét m ≠ 2

Hàm số có cực trị khi Δ'> 0 ⇔ m(m - 2) > 0 ⇔

Vậy m > 2 ∨ m < 0.

Ví dụ 3: Xác định các giá trị của tham số m để đồ thị hàm số y = mx⁴ - m² x² + 2016 có 3 điểm cực trị?

Hướng dẫn

Tập xác định D = R.

Tính y' = 4mx³ - 2xm².

Để hàm số có 3 điểm cực trị khi 

B. Bài tập vận dụng

Bài 1: Tìm m để hàm số y = mx³ + 3mx² - (m - 1)x - 1 có cực trị.

Bài 2: Tìm m để hàm số y = x³ - 3(m - 1)x² + 3(2m - 4)x + m có cực trị.

Bài 3: Tìm điều kiện của tham số m để hàm số y = x³ + mx² +(4m + 3)x + 2m - 1 có hai điểm cực trị.

Bài 4: Tìm các giá trị của m để hàm số y = x³ - 2mx + 4 không có điểm cực trị.

Bài 5: Tìm m để hàm số 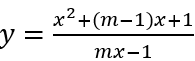có cực trị.

Bài 6:Tìm m để hàm số 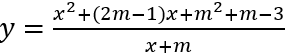 có cực trị.

Bài 7:Tìm m để hàm số y = x⁴ + 4mx³ + 3(m + 1)x² + 1 có ba cực trị

Bài 8:Tìm m để hàm số y = x⁴ + 4mx³ + 3(m + 1)x² + 1 có cực tiểu mà không có cực đại.