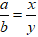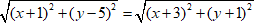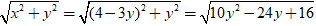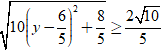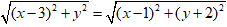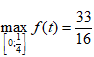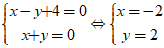Phương pháp giải Tìm giá trị lớn nhất, nhỏ nhất của số phức

1. Phương pháp giải

Để giải được các bài toán này . cần nắm được các kiên thức sau:

+ Bất đẳng thức tam giác

• |z₁ + z₂| ≤ |z₁| + |z₂|, dấu "=" khi z₁ = kz₂ với k ≥ 0. Dùng cho BĐT Mincopxki:

• |z₁ - z₂| ≤ |z₁| + |z₂|, dấu "=" khi z₁ = kz₂ với k ≤ 0. Dùng cho BĐT vecto

• |z₁ + z₂| ≤ ||z₁| - |z₂||, dấu "=" khi z₁ = kz₂ với k ≤ 0.

• |z₁ - z₂| ≤ ||z₁| - |z₂||, dấu "=" khi z₁ = kz₂ với k ≥ 0.

+ Bất đẳng thức khác

BĐT Cauchy: A² + B² ≥ 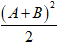 tìm min

BĐT Bunhia Copski:
(Ax + By)² ≤ (A² + B²)(x² + y²) tìm max

BĐT Mincopxki: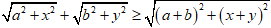
 tìm min. Dấu = xảy ra khi 

BĐT vecto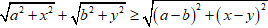
 tìm min. Dấu = xảy ra khi 

2. Ví dụ minh họa

Ví dụ 1: Trong các số phức z thỏa mãn điều kiện | z + 1- 5i| = | z− + 3 - i|, tìm số phức có môđun nhỏ nhất?

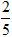
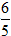
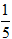
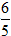
A. z =  +  i    B. z =  -  i

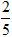
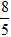
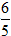
C. z = -  +  i    D. z =  -  i

Hướng dẫn:

Gọi số phức z = x + yi , (x,y ∈ R) ⇒ z− = x - yi

Ta có:

|z + 1 - 5i| = |z− + 3 - i| ⇔ |x + yi + 1 - 5i| = |x - yi + 3 - i|

⇔ |(x + 1) + (y - 5)i| = |(x + 3) + (-y - 1)i|

⇔ 

⇔ (x + 1)² +( y -5)² = ( x + 3)² + ( y + 1)²

⇔ x² + 2x + 1 + y² – 10y + 25
= x² + 6x+ 9 + y² + 2y + 1

⇔ - 4x – 12y + 16 = 0 ⇔ x + 3y – 4 = 0

⇔ x = 4 - 3y

Ta có modun của số phức z là:

|z| =

= 

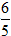
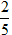
Đẳng thức xảy ra khi y =  ⇒ x =  .

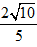
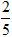
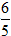
Vậy min|z| =  khi z =  +  i.

Chọn A.

Ví dụ 2: Trong các số phức z có phần thực , phần ảo không âm và thỏa mãn: 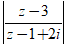 = 1 . Tìm số phức z sao cho biểu thức sau đạt giá trị lớn nhất
P = |z² - z− ²| - (z² - z− ²).i.[z(1 - i) + z−(1 + i)]

A. z =  + i    B. z =  +  i

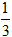
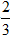
C. z =  +  i    D. z = 1 + i

Hướng dẫn:

Điều kiện: z ≠ 1 - 2i .

Gọi số phức cần tìm là z = x + yi,(x, y ∈ R; x,y > 0)

Theo giả thiết ta có:

 = 1 ⇔ |z - 3| = |z - 1 + 2i|.

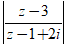
⇔ |x + yi - 3| = |x + yi - 1 + 2i|
⇔ |(x - 3) + yi| = |(x - 1) + (y + 2)i|

⇔ 

⇔ (x – 3)² + y² = (x - 1)² + ( y + 2)²

⇔ x² – 6x + 9 + y²
= x² – 2x + 1 + y² + 4y + 4

⇔ - 4x – 4y + 4 = 0 ⇔ x + y – 1 = 0

Số phức liên hợp với số phức z là:

z− = x - yi ⇒ z² - z− ² = 4xy.i
⇒ |z² - z− ²| = 4xy (vì x, y không âm)

z(1 - i) + z−(1 + i) = 2x + 2y

Do đó,
P = 16x²y² + 4xy.(2x+ 2y) = 16x²y² + 8xy.

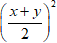
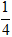
Đặt t = xy ⇒ 0 ≤ t ≤  =  , ta có
P = 16t² + 8t; t ∈ [0;  ] .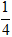

+ Xét hàm số f(t) = 16t² + 8t liên tục trên [0;  ] .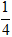

f'(t) = 32t + 8t; f'(t) = 0
⇔ t = 0 ∪ t = - 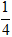 (loại)

f(0) = 0; f( ) =  ⇒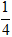 
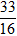
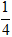
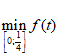
⇔ t =  ;  = 0 ⇔ t = 0

Khi t = 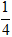 ⇒ xy = 

Lại có; x+ y – 1= 0 nên x = y =  .

Vậy P đạt giá trị lớn nhất bằng 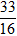 khi
z =  +  i .

Chọn C.

Ví dụ 3: Biết rằng số phức z thỏa mãn:
w = (z + 3 - i).(z− + 1 + 3i) là một số thực. Tìm giá trị nhỏ nhất của |z|?

A. √3    B. 2    C. 2√3    D. 2√2

Hướng dẫn:

Đặt z = x + yi (x, y ), số phức liên hợp với số phức z là z− = x - yi

Ta có: w = (z + 3 - i).(z− + 1 + 3i)

⇔ w = ( x + yi + 3 - i) . ( x - yi + 1 + 3i)

⇔ w = [ (x+ 3) + (y – 1).i ].[ (x+ 1)+ ( 3- y).i ]

⇔ w = ( x+ 3).(x+ 1) + ( x + 3). (3- y).i + ( y -1). ( x+ 1)i + ( y – 1). (3- y).i²

⇔ w = x² +4x + 3 + ( 3x - xy + 9 - 3y).i + (xy + y – x – 1).i - ( - y² + 4y – 3)

⇔ w = ( x² + 4x +3 + y² – 4y + 3) + ( 3x – xy + 9 – 3y + xy + y – x – 1).i

⇔ w = (x² + y² + 4x - 4y + 6) + ( 2x – 2y + 8).i

Để w là một số thực khi và chỉ khi
2x - 2y + 8 = 0 hay x - y + 4 = 0

⇒ Tập hợp các điểm biểu diễn của z là đường thẳng d: x – y + 4 = 0.

M(x;y) là điểm biểu diễn của z , z có môđun nhỏ nhất khi và chỉ khi độ dài OM nhỏ nhất

Khi và chỉ khi M là hình chiếu của O trên đường thẳng d.

⇒ OM ⊥ d

* Cách 1: Đường thẳng OM có dạng:
x + y + c = 0 .

Mà điểm O(0;0) thuộc đường thẳng OM nên ta có: 0 + 0 + c = 0 ⇒ c = 0

Do đó phương trình đường thẳng OM:
x + y = 0

Khi đó, tọa độ M là nghiệm hệ phương trình :

⇒ M(-2; 2) suy ra số phức cần tìm là
z = -2 + 2i.

⇒ |z| = 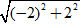 = 2√2

* Cách 2. Khi đó: |z| = d(O; d)
=  = 2√2

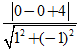
Chọn D.