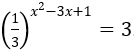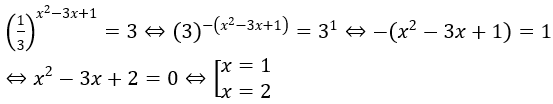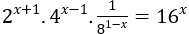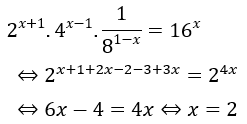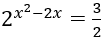Phương pháp đưa về cùng cơ số và phương pháp lôgarit hóa
Với Phương pháp đưa về cùng cơ số và phương pháp lôgarit hóa Toán lớp 12 với đầy đủ lý thuyết, phương pháp giải và bài tập có lời giải chi tiết giúp học sinh biết Phương pháp đưa về cùng cơ số và phương pháp lôgarit hóa .
Phương pháp đưa về cùng cơ số và phương pháp lôgarit hóa
A. Phương pháp giải & Ví dụ
1. Phương trình mũ cơ bản.
Phương trình mũ cơ bản có dạng: ax = m (1).
Nếu m > 0 thì phương trình (1) có nghiệm duy nhất x = logam.
Nếu m ≤ 0 thì phương trình (1) vô nghiệm.
2. Phương pháp đưa về cùng cơ số.
Với a > 0 và a ≠ 1 ta có af(x) = ag(x) ⇔ f(x) = g(x).
3. Phương pháp lôgarit hoá.
af(x) = b ⇔ f(x) = logab
af(x) = bg(x) ⇔ f(x) = g(x)logab
logaf(x) = b ⇔ f(x) = ab

Ví dụ minh họa
Bài 1: Giải phương trình sau
Hướng dẫn:
Bài 2: Giải phương trình sau
Hướng dẫn:
Bài 3: Giải phương trình sau
Hướng dẫn: