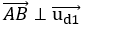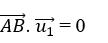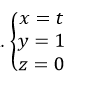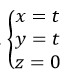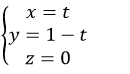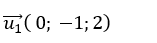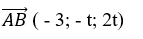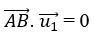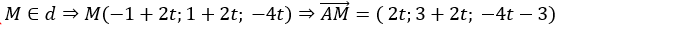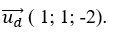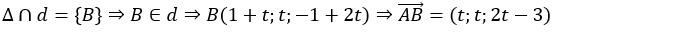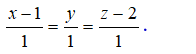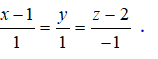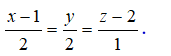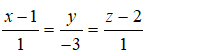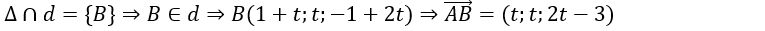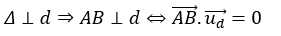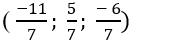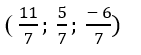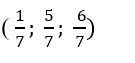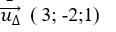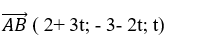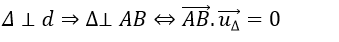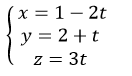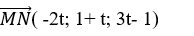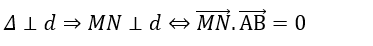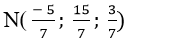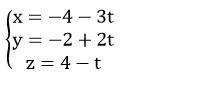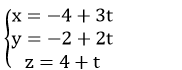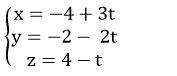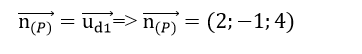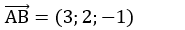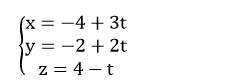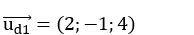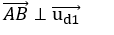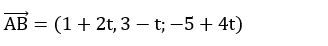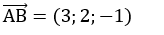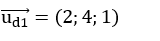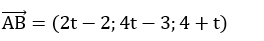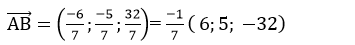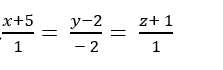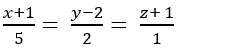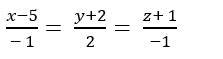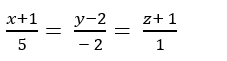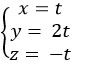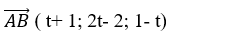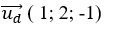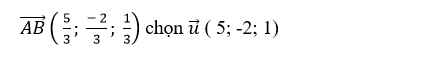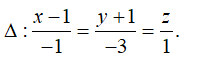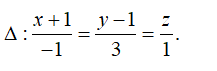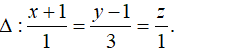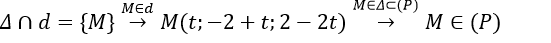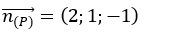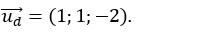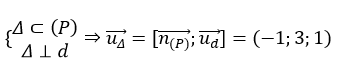Viết phương trình đường thẳng đi qua 1 điểm, cắt và vuông góc với đường thẳng

A. Phương pháp giải

Gọi giao điểm của đường thẳng d và d₁ là B.

+ Vì B thuộc đường thẳng d₁ nên tọa độ B có dạng... ( theo tham số t).

=> Tọa độ AB→

+ Xác định vecto chỉ phương u₁→  của đường thẳng d₁.

+ Do đường thẳng d vuông góc với đường thẳng d₁ nên 

=> 

=>Phương trình ẩn t ....=> t= ...

=> Tọa độ điểm B.

+ Viết phương trình đường thẳng d đi qua hai điểm A và B.

B. Ví dụ minh họa

Ví dụ 1. Cho đường thẳng d₁ có phương trình tham số: 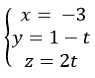 và điểm A(0;1; 0). Phương trình tham số đường thẳng d đi qua điểm A đồng thời vuông góc và cắt đường thẳng d₁ là:

A. 

B. 

C. 

D. Đáp án khác

Hướng dẫn giải

+Đường thẳng d₁ có vecto chỉ phương là: 

Gọi giao điểm của đường thẳng d và d₁ là B.

+ Vì B thuộc đường thẳng d1 nên tọa độ B có dạng B( -3;1-t;2t)

=> 

Vì đường thẳng d vuông góc với đường thẳng d₁ nên ta có: 

⇔ 

⇔ 0. (-3) – 1( - t) + 2.2t= 0 ⇔ 5t= 0 ⇔ t= 0

Suy ra tọa độ B( - 3; 1; 0)

+ Đường thẳng cần tìm chính là đường thẳng AB: đi qua A( 0;1; 0) và có vecto chỉ phương: 

Vậy phương trình tham số của đường thẳng d là:

Chọn A.

Ví dụ 2. Cho điểm A( -1; -2; 3) và đường thẳng d: 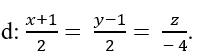 . Đường thẳng Δ đi qua cắt và vuông góc với đường thẳng d. Tìm một vecto chỉ phương của đường thẳng Δ

A . ( 4; 4; 0)

B. (2; -2; 1)

C. ( 2;4; 1)

D. ( 3; -3;0)

Hướng dẫn giải

Gọi giao điểm của đường thẳng d và Δ là M

Khi đó :

Đường thẳng d có vecto chỉ phương là: 

Khi đó :

⇔ 1. 2t+ 1( 3+ 2t) – 2( - 4t- 3) =0

⇔ 2t+ 3+ 2t+ 8t+ 6 = 0⇔ 12t + 9= 0

⇔ t= (-3)/4

Suy ra 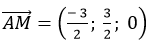 là một vecto chỉ phương của đường thẳng d.

Chọn D.

Ví dụ 3. Trong không gian với hệ toạ độ Oxyz,cho điểm A(1; 0;2) và đường thẳng d có phương trình 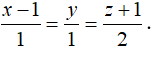 . Viết phương trình đường thẳng Δ đi qua A vuông góc và cắt d

A. 

B. 

C. 

D. 

Hướng dẫn giải

Ta có 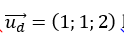 là một vecto chỉ phương của đường thẳng d.

Gọi :

Do 

⇔t+t+2(2t-3)=0⇔6t-6=0 nên t=1⇒ 

Đường thẳng Δ đi qua A và nhận 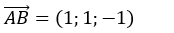 làm vectơ chỉ phương nên có phương trình 

Chọn B.

Ví dụ 4. Cho đường thẳng Δ có phương trình chính tắc: 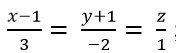 ; điểm A(-1;2; 0) . Đường thẳng d đi qua điểm A đồng thời vuông góc và cắt đường thẳng Δ tại điểm có tọa độ là?

A.

B. 

C.

D. 

Hướng dẫn giải

+ Ta có đường thẳng Δ có vecto chỉ phương 

Gọi giao điểm của đường thẳng d và Δ là B.

+ Vì B thuộc đường thẳng Δ nên tọa độ B có dạng B( 1+3t; -1-2t; t)

=> 

+ Do 

⇔ 3( 2+ 3t) – 2( - 3 -2t) + 1. t= 0

⇔ 6+ 9t + 6 + 4t + t= 0

⇔ 14t+ 12= 0 ⇔ t= (- 6)/7

=> Tọa độ giao điểm của d và Δ là 

Chọn A.

Ví dụ 5: Trong không gian với hệ tọa độ Oxyz; cho điểm M( 1;1;1) và đường thẳng d đi qua hai điểm A(1; 2;0) và B(-1;3;3). Gọi Δ là đưởng thẳng qua M vuông góc và cắt d. Biết rằng đường thẳng d và Δ cắt nhau tại 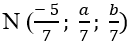 . Tính a+ b ?

A. 16

B. – 10

C. 18

D. -8

Hướng dẫn giải

+ Đường thẳng d đi qua hai điểm A( 1;2;0) và B( -1; 3;3) nên đường thẳng này nhận vecto 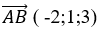 làm vecto chỉ phương

=> Phương trình đường thẳng d: 

+ Gọi N là giao điểm của Δ và d.

Do N thuộc đường thẳng d nên tọa độ N( 1- 2t; 2+ t; 3t)

=> 

+ Do 

⇔ - 2. (-2t) + 1. ( 1+ t) + 3( 3t-1) = 0 ⇔ 4t+ 1+ t+ 9t – 3 = 0⇔ 14t - 2= 0 ⇔ t= 1/7

=> Tọa độ điểm 

=> a= 15 và b= 3 nên a+ b= 18

Chon C.

Ví dụ 6: Cho điểm A (-4; -2; 4) và đường thẳng 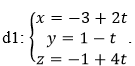 . Viết phương trình đường thẳng d đi qua A, cắt và vuông góc với đường thẳng d₁

A. 

B. 

C. 

D. 

Hướng dẫn giải

Chọn A

Cách 1:

- Mặt phẳng (P) đi qua điểm A và vuông góc với đường thẳng d₁ có vectơ pháp tuyến là

Phương trình mặt phẳng (P) là: 2.(x + 4) – 1 . (y + 2) + 4. (z – 4) = 0 hay 2x – y + 4z – 10 = 0

- Gọi giao điểm của ( P) và d1 là B( -3+ 2t; 1- t; - 1+ 4t) .

Thay tọa độ điểm B vào phương trình mặt phẳng ( P) ta được: 2( -3+ 2t)- ( 1-t)+ 4(- 1+4t) – 10= 0 ⇔ - 6+ 4t – 1+ t – 4+ 16t – 10=0 ⇔ 21t – 21= 0 ⇔ t= 1 => B (-1; 0; 3)

- Đường thẳng cần tìm là đường thẳng đi qua 2 điểm A, B

Vectơ chỉ phương của d là: 

Vậy phương trình đường thẳng d là: 

Cách 2:

Vecto chỉ phương của đường thẳng d₁ là: 

Gọi B là giao điểm của d và d₁, vì d vuông góc với d₁ nên 

Tọa độ của B (-3+2t; 1-t;-1+4t)

=> 

⇔2(1+2t)-(3-t)+4(-5+4t)=0

⇔t=1

=> 

Vậy phương trình của d là :

Ví dụ 7: Cho điểm A (2; 3; -1) và đường thẳng 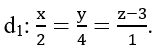 . Đường thẳng d đi qua A, cắt và vuông góc với đường thẳng d₁. Trong các vecto sau vecto nào không là vecto chỉ phương của đường thẳng d?

A ( 6; 5; -32)

B. ( 6; -5; 16)

C. ( - 12; -10; 64)

D. ( -18; -15; 96)

Hướng dẫn giải

+ Đường thẳng d₁ có vecto chỉ phương 

+ Gọi B là giao điểm của d và d₁, vì d vuông góc với d₁ nên 

Tọa độ của B (2t; 4t;3+t)

=> 

+  ⇔t=4/7

=>

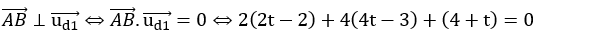
+ Ta thấy các vecto trong các phương án A; C; D cùng phương với vecto AB→  nên các vecto trong các phương án A; C và D cũng là vecto chỉ phương của đường thẳng d.

Chọn B.

Ví dụ 8:Trong không gian với hệ tọa độ Oxyz; cho đường thẳng d đi qua hai điểm O và M( 1; 2; -1). Phương trình chính tắc của đường thẳng đi qua điểm A(-1;2;-1), cắt và vuông góc với d là:

A.

B.

C. 

D. 

Hướng dẫn giải

+ Gọi Δ là đường thẳng cần tìm. Gọi giao điểm của d và Δ là B.

+ Đường thẳng d đi qua hai điểm O và M (1; 2; -1) nên đường thẳng này nhận vecto 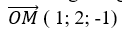 làm vecto chỉ phương.

=> Phương trình đường thẳng d: 

+ Do B thuộc d nên tọa độ B( t; 2t; - t) => 

+ Đường thẳng d có vectơ chỉ phương 

+ Do 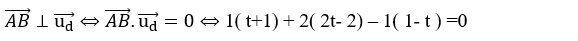 ⇔ t+ 1 + 4t – 4- 1+ t= 0 ⇔ 6t – 4= 0 nên t= 2/3

+ Đường thẳng Δ đi qua điểm A( -1;2; -1) và có vectơ chỉ phương 

Vậy phương trình của Δ là: 

Chọn D.

Ví dụ 9: Trong không gian với hệ tọa độ Oxyz, đường thẳng Δ nằm trong mặt phẳng (P): 2x+ y- z -1= 0. Biết Δ vuông góc và cắt đường thẳng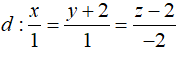 . Phương trình đường thẳng Δ là:

A.

B.

C. 

D. 

Hướng dẫn giải

Gọi

Thay tọa độ điểm M vào phương trình ( P) ta được: ⇒2t-2+t-(2-2t)-1=0⇔5t-5=0 ⇔ t=1⇒M(1;-1;0)∈Δ.

Ta có Vecto pháp tuyến của (P) là : 

Vecto chỉ phương của đường thẳng d là 

Khi đó 

⇒ .

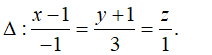
Chọn C.