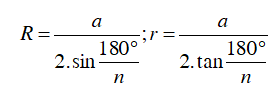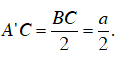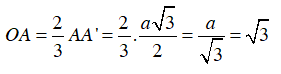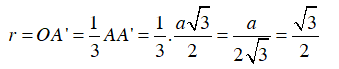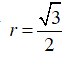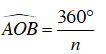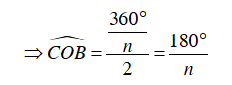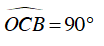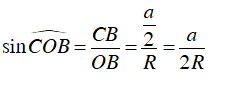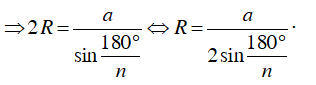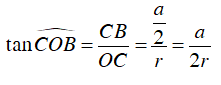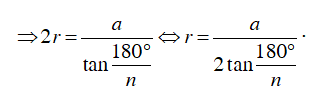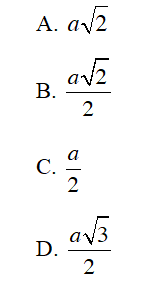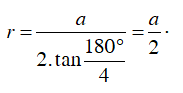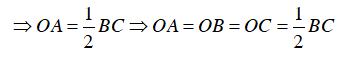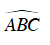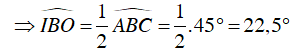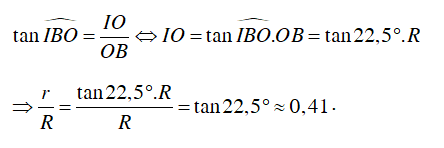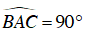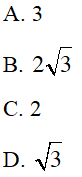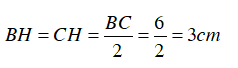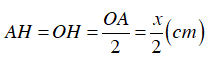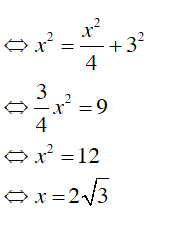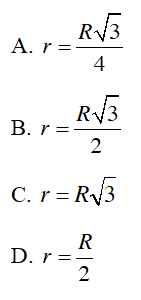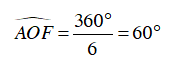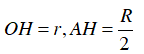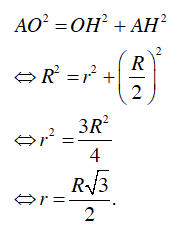Cách xác định tâm và bán kính đường tròn ngoại tiếp, đường tròn nội tiếp

A. Phương pháp giải

+ Đa giác đều n cạnh có độ dài mỗi cạnh là a, R là bán kính đường tròn ngoại tiếp và r là bán kính đường tròn nội tiếp đa giác. Ta có:

+ Ngoài ra có thể sử dụng hệ thức lượng trong tam giác vuông, định lý Py – ta – go,… để tính R và r.

B. Ví dụ minh họa

Ví dụ 1 :

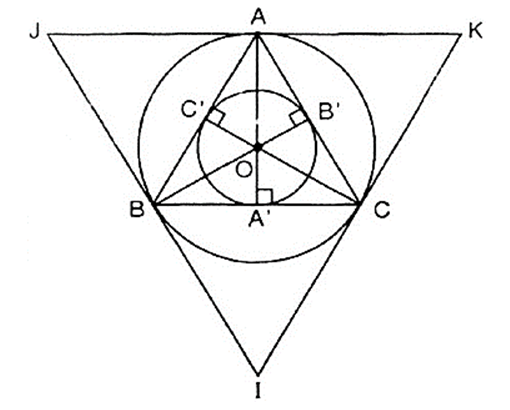
a) Vẽ tam giác đều ABC cạnh a = 3cm.

b) Vẽ tiếp đường tròn (O; R) ngoại tiếp tam giác đều ABC. Tính R.

c) Vẽ tiếp đường tròn (O; r) nội tiếp tam giác đều ABC. Tính r.

d) Vẽ tiếp tam giác đều IJK ngoại tiếp đường tròn (O; R).

Hướng dẫn giải

a) Vẽ tam giác đều ABC có cạnh bằng 3cm (dùng thước thẳng và compa).

+ Dựng đoạn thẳng AB = 3cm .

+ Dựng cung tròn (A, 3) và cung tròn (B, 3). Hai cung tròn này cắt nhau tại điểm C.

Nối A với C, B với C ta được tam giác đều ABC cạnh 3cm.

b) * Vẽ đường tròn:

Tâm O của đường tròn ngoại tiếp tam giác đều ABC là giao điểm của ba đường trung trực.

Dựng đường trung trực của đoạn thẳng BC và CA.

Hai đường trung trực cắt nhau tại O.

Vẽ đường tròn tâm O, bán kính OA = OB = OC ta được đường tròn ngoại tiếp tam giác ABC.

* Tính bán kính đường tròn.

+ Gọi A’ là trung điểm BC ⇒ 

và AA’ ⊥ BC

⇒  .

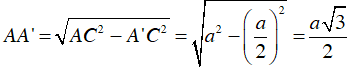
+ Do tam giác ABC là tam giác đều nên 3 đường trung trực đồng thời là ba đường trung tuyến

⇒ Giao điểm ba đường trung trực cũng là giao điểm ba đường trung tuyến

Suy ra O là trọng tâm tam giác ABC.

⇒ 

Vậy R = 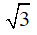 (cm).

c) * Vẽ đường tròn:

Gọi A’; B’; C’ lần lượt là chân đường phân giác trong ứng với các góc 

Do tam giác ABC là tam giác đều nên A’; B’; C’ đồng thời là trung điểm BC; CA; AB.

Đường tròn (O; r) là đường tròn tâm O; bán kính OA’ = OB’ = OC’.

* Tính r:

Vậy 

d) Vẽ các tiếp tuyến với đường tròn (O; R) tại A, B, C. Ba tiếp tuyến này cắt nhau tại I, J, K. Ta có ΔIJK là tam giác đều ngoại tiếp (O; R).

Ví dụ 2 : Cho một đa giác đều n cạnh có độ dài mỗi cạnh là a. Hãy tính bán kính R của đường tròn ngoại tiếp và bán kính r của đường tròn nội tiếp đa giác đều đó

Hướng dẫn giải

Giả sử: OA = OB = R, OC = r

Ta có: 

Trong tam giác COB, ta có: 

Nên 

Ta lại có 

Ví dụ 3 :

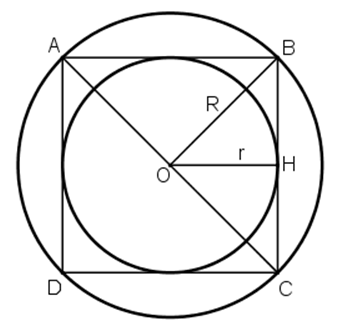
a) Vẽ đường tròn tâm O, bán kính 2cm.

b) Vẽ hình vuông nội tiếp đường tròn (O) ở câu a).

c) Tính bán kính r của đường tròn nội tiếp hình vuông ở câu b) rồi vẽ đường tròn (O; r).

Hướng dẫn giải

a) Chọn điểm O là tâm, mở compa có độ dài 2cm vẽ đường tròn tâm O, bán kính 2cm.

b) Vẽ đường kính AC và BD vuông góc với nhau. Nối A với B, B với C, C với D, D với A ta được tứ giác ABCD là hình vuông nội tiếp đường tròn (O; 2cm).

c) Vẽ OH ⊥ BC.

⇒ OH là khoảng cách từ tâm O đến BC

Vì AB = BC = CD = DA ( ABCD là hình vuông) nên khoảng cách từ tâm O đến AB, BC, CD, DA bằng nhau ( định lý lien hệ giữa dây cung và khoảng cách từ tâm đến dây)

⇒ O là tâm đường tròn nội tiếp hình vuông ABCD

OH là bán kính r của đường tròn nội tiếp hình vuông ABCD.

Tam giác vuông OBC có OH là đường trung tuyến ⇒  .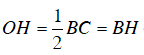

Xét tam giác vuông OHB có :  .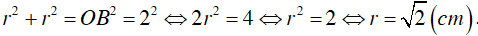

Vẽ đường tròn (O; OH). Đường tròn này nội tiếp hình vuông, tiếp xúc bốn cạnh hình vuông tại các trung điểm của mỗi cạnh.

C. Bài tập trắc nghiệm

Câu 1 : Đường tròn nội tiếp hình vuông cạnh a có bán kính là

Hướng dẫn giải

Đáp án C

Áp dụng công thức: 

Câu 2 : Hình nào trong các hình dưới đây không có đường tròn nội tiếp

A. Hình chữ nhật

B. Hình vuông

C. Hình tam giác

D. Hình tam giác đều

Hướng dẫn giải

Đáp án A

Hình chữ nhật chỉ có đường tròn ngoại tiếp, không có đường tròn nội tiếp.

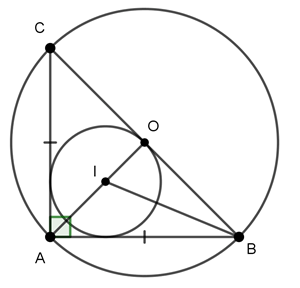
Câu 3 : Cho tam giác ABC vuông cân tại A. Gọi R là bán kính đường tròn ngoại tiếp; r là bán kính đường tròn nội tiếp tam giác ABC. Tính tỉ số 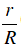 (làm tròn đến số thập phân thứ hai).

A. 0,5

B. 0,44

C. 0,41

D. 0,42

Hướng dẫn giải

Đáp án C

Tam giác ABC vuông cân tại A, gọi O là trung điểm của BC

⇒ O là tâm đường tròn ngoại tiếp tam giác ABC

Gọi I là tâm đường tròn nội tiếp tam giác ABC

⇒ I thuộc phân giác góc BAC

Mà tam giác ABC vuông cân tại A nên đường trung tuyến AO trùng với đường phân giác AI, hơn nữa AO BC.

Ta có BI là tia phân giác của 

Xét ΔIOB vuông tại O, ta có:

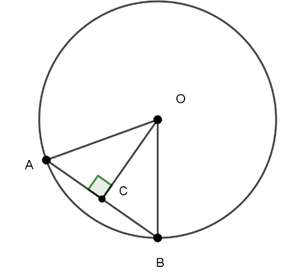
Câu 4 : Cho tam giác ABC có AB = 6cm; BC= 10 cm và AC = 8cm. Tâm đường tròn ngoại tiếp tam giác ABC là điểm nào?

A. Trung điểm AB

B. Trung điểm BC

C. Trung điểm AC

D. Trọng tâm tam giác ABC

Hướng dẫn giải

Đáp án B

Xét ΔABC , có:

BC² = 10² = 100

AB² + AC² = 6² + 8² = 100

⇒ BC² = AB² + AC²

Theo định lý Py – ta – go đảo suy ra tam giác ABC vuông tại A

⇒ 

⇒ A, B, C nội tiếp đường tròn đường kính BC hay đường tròn ngoại tiếp tam giác ABC có tâm là trung điểm của BC.

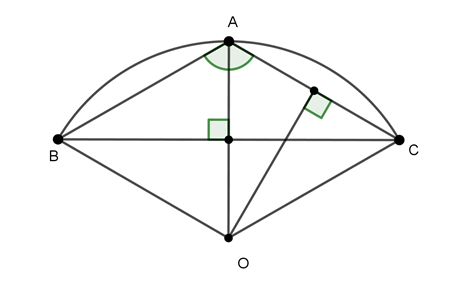
Câu 5 : Cho tam giác ABC cân tại A, có 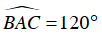 và BC = 6cm. Tính bán kính đường tròn ngoại tiếp tam giác ABC.

Hướng dẫn giải

Đáp án B

Gọi O là tâm đường tròn ngoại tiếp tam giác ABC, H là giao điểm của OA và BC

Xét tam giác OAC, có OA = OC

Suy ra tam giác OAC cân tại O

Ta có ΔABC cân tại A

AO là tia phân giác của 

⇒ 

⇒ ΔOAC đều

Đặt OA = OC = AC = x,

Vì OA là đường trung trực của BC nên H là trung điểm của BC

⇒ 

Vì CH ⊥ OA nên CH cũng là đường trung tuyến nên H là trung điểm của AO

⇒ 

Xét ΔCHA vuông tại H, ta có :

AC² = AH² + CH² (định lý Py – ta – go)

Vậy bán kính đường tròn ngoại tiếp tam giác ABC là  .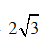

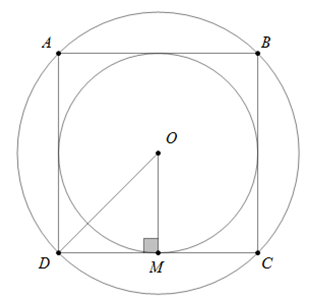
Câu 6 : Cho hình vuông sau,

Nhận xét nào sau đây đúng?

A. Bán kính đường tròn ngoại tiếp luôn lớn hơn bán kính đường tròn nội tiếp của hình vuông đó.

B. Bán kính đường tròn ngoại tiếp luôn bằng bán kính đường tròn nội tiếp của hình vuông đó.

C. Bán kính đường tròn ngoại tiếp luôn nhỏ hơn bán kính đường tròn nội tiếp của hình vuông đó.

D. Bán kính đường tròn ngoại tiếp luôn bằng một nửa bán kính đường tròn nội tiếp của hình vuông đó.

Hướng dẫn giải

Đáp án A

Hướng dẫn giải

Xét hình vuông ABCD có tâm O, kẻ OM ⊥ CD (M ∈ CD)

Lúc đó OD là bán kính đường tròn ngoại tiếp, OM là bán kính đường tròn nội tiếp hình vuông ABCD

ΔOMD vuông tại M nên OD ≥ OM (1)

Giả sử OD = OM khi đó đường tròn nội tiếp và đường tròn ngoại tiếp là hai đường tròn có chung tâm O và độ dài hai bán kính bằng nhau nên chúng trùng nhau.

Lúc đó không tồn tại hình vuông vừa có đỉnh trên đường tròn (O) vừa có cạnh tiếp xúc với đường tròn (O)

Do đó OD ≠ OM kết hợp với (1) ta có OD > OM (đpcm).

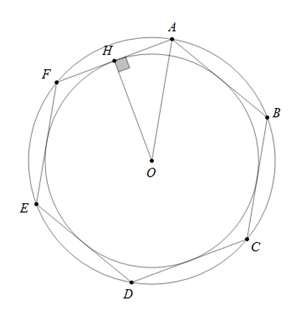
Câu 7 : Cho lục giác đều ABCDEF có tâm O. Đặt R, r lần lượt là bán kính đường tròn ngoại tiếp và nội tiếp lục giác. Viết biểu thức liên hệ giữa R và r.

Hướng dẫn giải

Đáp án B

Lục giác đều ABCDEF nên chia đường tròn ngoại tiếp thành 6 cung bằng nhau, suy ra

Tam giác AOF cân tại O có 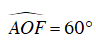 nên ΔAOF đều

Vẽ đường cao AH của ΔAOF

Khi đó 

Xét ΔAOH vuông tại H nên