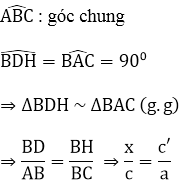Cách giải bài tập Hệ thức về cạnh và đường cao trong tam giác vuông cực hay

Lý thuyết và Phương pháp giải

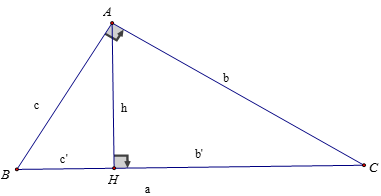
    Cho ΔABC, góc A bằng 90⁰, AH ⊥ BC, AB = c, AC = b, BC = a, AH = h thì:

        + BH = c' được gọi là hình chiếu của AB xuống BC

        + CH = b' được gọi là hình chiếu của AC xuống BC

    Khi đó, ta có:

    1) AB² = BH.BC hay c² = a.c'

    AC² = CH.BC hay b² = a.b'

    2) AH² = CH.BH hay h² = b'.c'

    3) AB.AC = AH.BC hay b.c = a.h

    5) AB² + AC² = BC² hay b² + c² = a² (Định lý Pytago)

Ví dụ minh họa

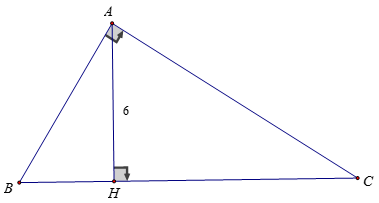
Ví dụ 1: Cho tam giác ABC vuông tại A, AB < AC. Biết AH = 6 cm, HC – HB = 3,5 cm. Tính độ dài AB, AC

Hướng dẫn:

    Ta có: AH² = BH.CH ⇒ BH.CH = 36

    Mặt khác: CH - BH = 3,5 (1)

    ⇒ (CH - BH)² = 3,5² = 12,25

    Ta có: (CH + BH)² = (CH - BH)² + 4BH.CH = 12,25 + 4.36 = 156,25

    ⇒ CH + BH = √156,25 = 12,5 (2)

    Từ (1) và (2) ⇒ CH = 8; BH = 4,5

    Ta có: AB² = BH.BC = 4,5.12,5 = 56,25 ⇒ AB = 7,5 (cm)

    AC² = CH.BC = 8.12,5 = 100 ⇒ AB = 10 (cm)

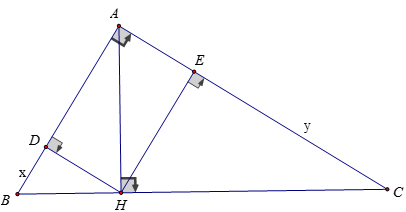
Ví dụ 2: Cho tam giác ABC vuông tại A, đường cao AH. Gọi D, E là hình chiếu của H trên AB và AC. Đặt BC = a; CA = b; AB = c; AH = h; BD = x; CE = y. Chứng minh rằng:

    a) a²x = c³; a²y = b³

    b) axy = h³

Hướng dẫn:

    a) Đặt BH = c'; CH = b'

    Xét ΔBDH và ΔBAC có:

    ⇒ a.x = c.c'

    ⇒ a.a.x = a.c.c' hay a²x = a.c.c'

    Mặt khác a.c' = c² nên a²x = c.c² ⇒ a²x = c³

    Chứng minh tương tự, ta được a²y = b³

    b) Ta có: a²x.a²y = c³.b³

    Lại có: b.c = a.h nên a⁴.xy = a³h³

    ⇒ a.xy = h³

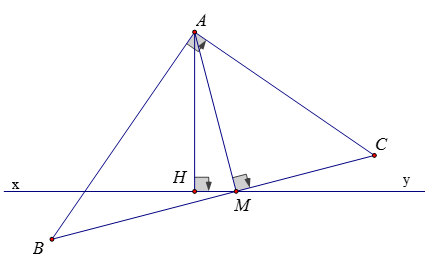
Ví dụ 3: Cho điểm A nằm ngoài đường thẳng xy và cách đường thẳng xy là 3 cm. Gọi M là điểm di động trên xy. Vẽ tam giác ABC vuông tại A sao cho AM là đường cao của tam giác đó. Tính giá trị nhỏ nhất của tích MB.MC

Hướng dẫn:

    Gọi H là hình chiếu của A trên xy, H là điểm cố định và AH = 3cm

    Ta có: AM ≥ AH ( dấu bằng xảy ra khi M trùng H)

    Xét tam giác ABC vuông tại A có AM là đường cao nên :

    MB.MC = AM² ≥ AH² = 3² = 9

    Do đó, tích MB. MC đạt giá trị nhỏ nhất là 9 khi M trùng H