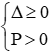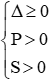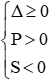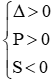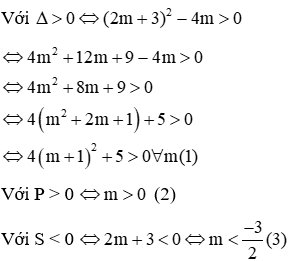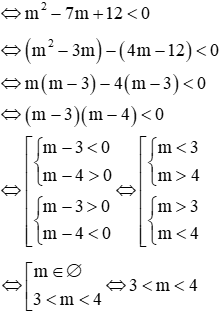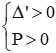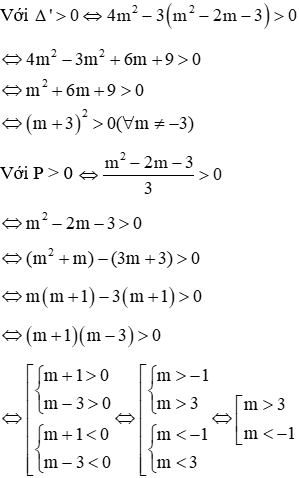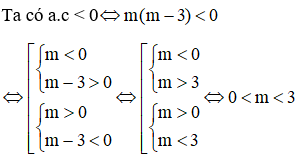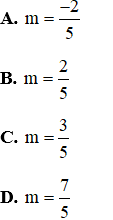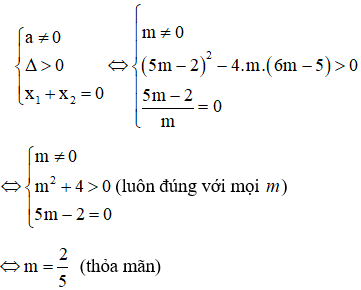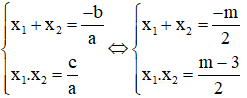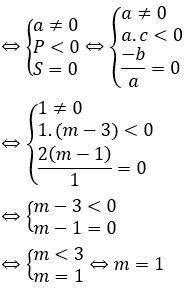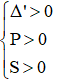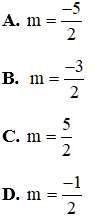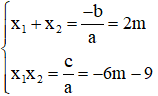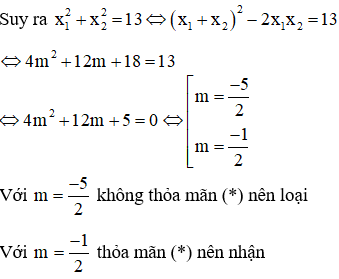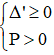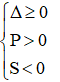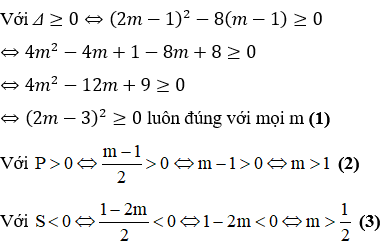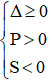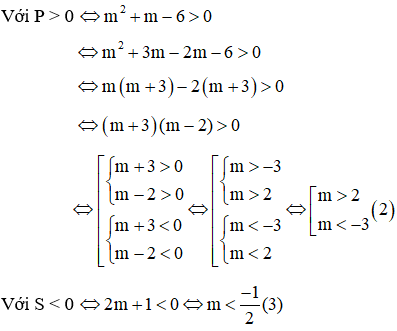Tìm m để phương trình bậc hai có hai nghiệm cùng dấu, trái dấu

A. Phương pháp giải

- Cho phương trình ax² + bx + c = 0 (a ≠ 0). Khi đó

+ Điều kiện để phương trình có 2 nghiệm trái dấu: a.c < 0

+ Điều kiện để phương trình có 2 nghiệm cùng dấu: 

( nếu là 2 nghiệm phân biệt cùng dấu ta thay ∆ ≥ 0 bởi ∆ > 0)

+ Điều kiện để phương trình có 2 nghiệm cùng dấu dương: 

( nếu là 2 nghiệm phân biệt cùng dấu ta thay ∆ ≥ 0 bởi ∆ > 0)

+ Điều kiện để phương trình có 2 nghiệm cùng dấu âm: 

( nếu là 2 nghiệm phân biệt cùng dấu ta thay ∆ ≥ 0 bởi ∆ > 0)

Ví dụ 1: Tìm m để phương trình  x² – (2m + 3)x + m = 0 có hai nghiệm phân biệt cùng dấu âm < /p>

Giải

Phương trình có 2 nghiệm phân biệt cùng dấu âm khi 

Không có giá trị nào của m thỏa mãn (1), (2) và (3)

Vậy không tồn tại m thỏa mãn đề bài

Ví dụ 2: Tìm m để phương trình  x² – (m² + 1)x + m² – 7m + 12 = 0 có hai nghiệm trái dấu

Giải

Phương trình có 2 nghiệm trái dấu khi a.c < 0

Vậy với 3 < m < 4 thì phương trình có hai nghiệm trái dấu

Ví dụ 3: Tìm m để phương trình  3x² – 4mx + m < ² – 2m - 3 = 0 có hai nghiệm phân biệt cùng dấu

Giải

Phương trình có 2 nghiệm phân biệt cùng dấu khi 

Vậy với m > 3 hoặc m < -1 thì phương trình có hai nghiệm phân biệt cùng dấu

B. Bài tập

Câu 1: Cho phương trình mx² + 2(m - 2)x + m - 3 = 0. Xác định m để phương trình có hai nghiệm trái dấu.

A. m > 0          

B. 1 < m < -1

C. 0

D. m < 3

Giải

Để phương trình có hai nghiệm trái dấu thì m ≠ 0 và a.c < 0

Suy ra các giá trị m cần tìm là 0 < m < 3

Đáp án đúng là C

Câu 2: Tìm m để phương trình  mx² – (5m – 2)x + 6m – 5 = 0 có hai nghiệm đối nhau.

Giải

Xét phương trình: mx² - (5m - 2)x + 6m - 5 = 0

Để để phương trình có hai nghiệm đối nhau thì:

Vậy 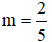 thì phương trình có hai nghiệm đối nhau.

Đáp án đúng là B

Câu 3: Tìm  giá trị m để phương trình 2x² + mx + m - 3 = 0 có 2 nghiệm trái dấu và nghiệm âm có giá trị tuyệt đối lớn hơn nghiệm dương.

A. 0 < m < 3

B. -1 < m < 3             

C. m < 2    

D. m > -3

Giải

Để phương trình có hai nghiệm trái dấu thì: a.c < 0 ⇔ 2.(m-3) < 0 ⇔ m < 3  (1)

Giả sử phương trình có hai nghiệm trái dấu: x₁ < 0 < x₂

Với m < 3 , áp dụng hệ thức Vi- ét ta có:

Vì nghiệm âm có giá trị tuyệt đối lớn hơn nghiệm dương nên:

|x₁| > |x₂| trong đó x₁ < 0; x₂ > 0 nên 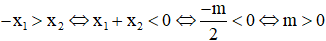 (2)

Từ (1) và (2) suy ra 0 < m < 3

Vậy 0 < m < 3 thì phương trình có hai nghiệm trái dấu và nghiệm âm có giá trị tuyệt đối lớn hơn nghiệm dương.

Đáp án đúng là A

Câu 4: Tìm  giá trị m để phương trình  x² – 2(m – 1)x + m – 3 = 0 có 2 nghiệm trái dấu và bằng nhau về giá trị tuyệt đối.

A. m = 1             

B. m = 4

C. m = 2

D. m = -3

Giải

Xét phương trình: x² – 2(m – 1)x + m – 3 = 0 có: a = 1, b = -2(m – 1), c = m – 3

Phương trình có 2 nghiệm trái dấu và bằng nhau về giá trị tuyệt đối

Vậy với m = 1 thì phương trình đã cho có hai nghiệm trái dấu và bằng nhau về giá trị tuyệt đối.

Đáp án đúng là A

Câu 5: Cho phương trình: x² - 2mx + 2m - 4 = 0. Có bao nhiêu giá trị nguyên của m nhỏ hơn 2020 để phương trình có 2 nghiệm dương phân biệt.

A. 2016

B. 2017                  

C. 2018

D. 2019

Giải

Phương trình có 2 nghiệm phân biệt cùng dấu dương khi 

Với Δ' > 0 ⇔ m² - (2m - 4) > 0 ⇔ (m² - 2m + 1) + 3 > 0 ⇔ (m - 1)² + 3 > 0 ∀ m(1)

Với P > 0 ⇔ 2m - 4 > 0 ⇔ m > 2(2)

Với S > 0 ⇔ 2m > 0 ⇔ m > 0(3)

Từ (1), (2), (3) ta có các giá trị m cần tìm là m > 2

Suy ra số các giá trị nguyên của m thỏa mãn: 2 < m < 2020 có 2017 số

Đáp án đúng là B

Câu 6: Cho phương trình: x² - 2mx - 6m - 9 = 0. Tìm m để phương trình có 2 nghiệm trái dấu thỏa mãn x₁²+x₂²=13

Giải

Phương trình có 2 nghiệm trái dấu khi: 

Theo Vi-et ta có: 

Đáp án đúng là D

Câu 7: Cho phương trình: x² - 8x + m + 5 = 0. Gọi S là tập hợp chứa tất cả các giá trị nguyên của m để phương trình có 2 nghiệm cùng dấu. Tính tổng tất cả các phần tử của S

A. 30               

B. 56             

C. 18            

D. 29

Giải

Phương trình có 2 nghiệm cùng dấu khi 

Với Δ' ≥ 0 ⇔ 16 - m - 5 ≥ 0 ⇔ 11-m ≥ 0 ⇔ m ≤ 11 (1)

Với P > 0 ⇔ m + 5 > 0 ⇔ m > -5(2)

Từ (1), (2) ta có các giá trị m cần tìm là -5 < m ≤ 11

Suy ra S = {-4,-3,-2,-1,0,1,2,3,4,5,6,7,8,9,10,11}

Vậy tổng tất cả các phần tử của S là 56

Đáp án đúng là B

Câu 8: Cho phương trình: 2x² + (2m - 1)x + m - 1 = 0. Tìm m để phương trình có 2 nghiệm âm.

A. m > 3               

B. m < -1             

C. m > 1               

D. m < -3

Giải

Phương trình có 2 nghiệm cùng dấu âm khi 

Từ (1), (2), (3) ta có các giá trị của m cần tìm là: m > 1

Đáp án đúng là C

Câu 9: Cho phương trình x² - 2x - 1 = 0 (m là tham số). Tìm khẳng định đúng

A. Phương trình luôn có hai nghiệm trái dấu.

B. Phương trình vô nghiệm < /p>

C. Phương trình có hai nghiệm cùng dấu

D. Phương trình có nghiệm kép

Giải

Vì ac = 1.(-1) = -1 < 0 nên phương trình có 2 nghiệm trái dấu

Đáp án đúng là A

Câu 10: Cho phương trình x² - (2m + 1)x + m² + m - 6 = 0. Tìm m để phương trình có 2 nghiệm âm.

A. m > 2               

B. m < -4             

C. m > 6               

D. m < -3

Giải

Phương trình có 2 nghiệm cùng dấu âm khi 

Δ = (2m + 1)² - 4(m² + m - 6) = 4m² + 4m + 1 - 4m² - 4m + 24 = 25 > 0 với mọi giá trị của m(1)

Suy ra m < -3 đồng thời thỏa mãn (1), (2) và (3)

Vậy m < -3 thỏa mãn đề bài.

Đáp án đúng là D