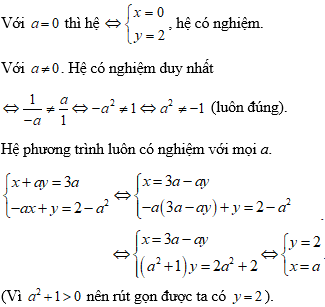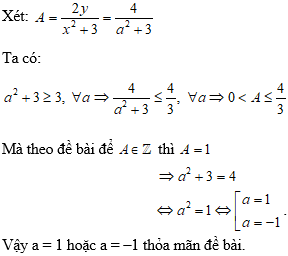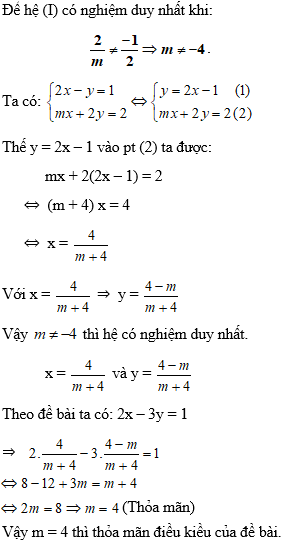Tìm điều kiện của m để hệ phương trình có nghiệm duy nhất cực hay
Với Tìm điều kiện của m để hệ phương trình có nghiệm duy nhất cực hay Toán học lớp 9 với đầy đủ lý thuyết, phương pháp giải và bài tập có lời giải cho tiết sẽ giúp học sinh nắm được Tìm điều kiện của m để hệ phương trình có nghiệm duy nhất cực hay.
Tìm điều kiện của m để hệ phương trình có nghiệm duy nhất cực hay
A. Phương pháp giải
Phương pháp:
Bước 1: Tìm điều kiện của m để hệ có nghiệm duy nhất sau đó giải hệ phương trình tìm nghiệm (x;y) theo tham số m.
Bước 2: Thế x và y vừa tìm được vào biểu thức điều kiện, sau đó giải tìm m.
Bước 3: Kết luận.
B. Ví dụ minh họa
Ví dụ 1: Cho hệ phương trình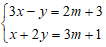 
(m là tham số).
Tìm m để hệ phương trình có nghiệm (x;y) thỏa mãn x2 + y2 = 5.
Hướng dẫn:
Vì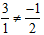 
nên hệ phương trình luôn có nghiệm duy nhất (x;y).
Vậy m = 1 hoặc m = –2 thì phương trình có nghiệm thỏa mãn đề bài.
Ví dụ 2: Cho hệ phương trình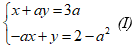 
(a là tham số).
Tìm a để hệ phương trình có nghiệm duy nhất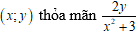 
là số nguyên.
Hướng dẫn:
Hệ phương trình luôn có nghiệm duy nhất (x;y) = (a;2).
Ví dụ 3: Cho hệ phương trình: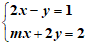 
(I) (m là tham số).
Tìm m đề hệ phương trình có nghiệm duy nhất sao cho 2x – 3y = 1.
Hướng dẫn:
Bài viết liên quan
- Cách giải hệ phương trình bằng phương pháp đặt ẩn phụ cực hay
- Cách giải hệ phương trình bậc nhất hai ẩn chứa tham số cực hay
- Cách tìm hệ thức liên hệ giữa x và y không phụ thuộc vào m của hệ phương trình
- Cách giải hệ phương trình đối xứng loại 1 cực hay
- Cách giải hệ phương trình đối xứng loại 2 cực hay
