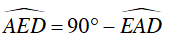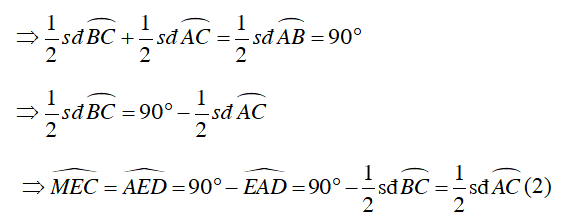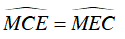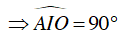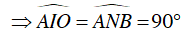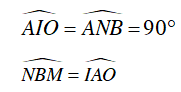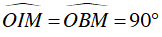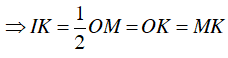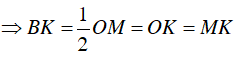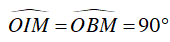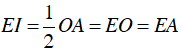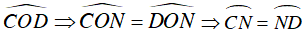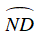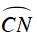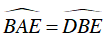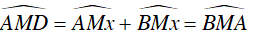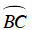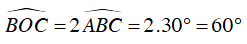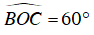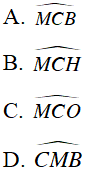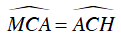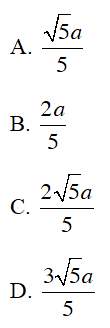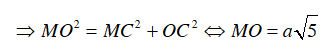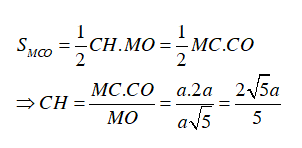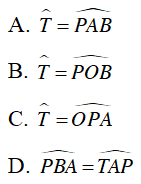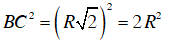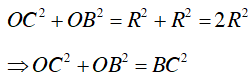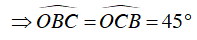Cách giải bài tập Góc tạo bởi tia tiếp tuyến và dây cung cực hay, chi tiết

A. Phương pháp giải

1. Định nghĩa

Cho xy là tiếp tuyến tại A với đường tròn (O).

Góc 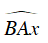 có đỉnh A nằm trên đường tròn, cạnh Ax là một tia tiếp tuyến còn cạnh kia chứa dây cung AB.

Góc 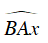 được gọi là góc tạo bởi tia tiếp tuyến và dây cung.

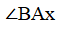
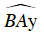
Dây AB căng hai cung. Cung nằm bên trong góc là cung bị chắn. Trên hình vẽ, góc  có cung bị chắn là cung nhỏ AB , góc  có cung bị chắn là cung lớn AB.

2. Số đo của góc tạo bởi tia tiếp tuyến và dây cung bằng nửa số đo của cung bị chắn.

3. Trong một đường tròn, góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn một cung thì bằng nhau.

B. Ví dụ minh họa

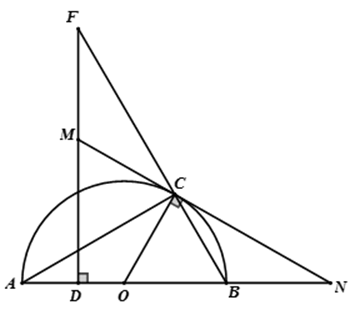
Ví dụ 1 : Cho điểm C thuộc nửa đường tròn (O) đường kính AB. Từ điểm D thuộc đọan AO kẻ đường thẳng vuông góc với AO cắt AC và BC lần lượt lại E và F. Tiếp tuyến C với nửa đường tròn cắt EF tại M và cắt AB tại N.

a) Chứng minh M là trung điểm của EF.

b) Tìm vị trí của điểm C trên đường tròn (O) sao cho ΔACN cân tại C.

Hướng dẫn giải

a) Ta có 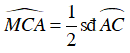 (góc giữa tiếp tuyến và dây cung chắn cung AC) (1)

Ta lại có: 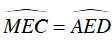 (hai góc đối đỉnh)

Xét tam giác AED vuông tại D, ta có:

 ( góc  là góc nội tiếp chắn cung  )

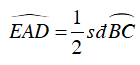
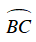
Mà 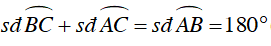 (cung AB là cung chắn nửa đường tròn có số đo bằng 180^o )

Từ (1) và (2) suy ra 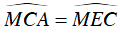 hay 

Vậy ΔMEC cân tại M, suy ra MC = ME.

Chứng minh tương tự ta có MC = MF.

Suy ra ME = MF hay M là trung điểm của EF.

b) ΔACN cân tại C khi và chỉ khi 

Vì MN là tiếp tuyến với (O) tại C nên OC ⊥ MN ⇒ 

Mà 

Vậy ΔACN cân tại C khi C là điểm nằm trên đường tròn sao cho  .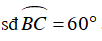

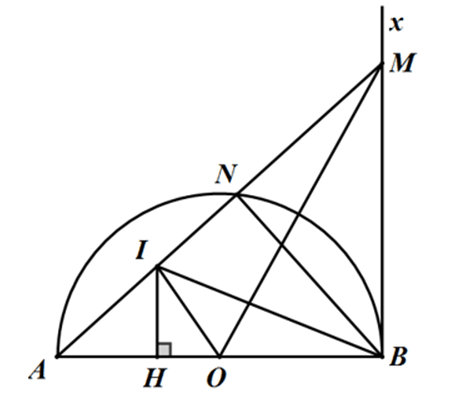
Ví dụ 2 : Cho nửa đường tròn (O) đường kính AB = 2R. Gọi M là một điểm thay đổi trên tiếp tuyến Bx của (O). Nối AM cắt (O) tại N. Gọi I là trung điểm của AN.

a) Chứng minh: ΔAIO ∼ ΔBMN ; ΔOBM ∼ ΔINB

b) Tìm vị trí của điểm M trên tia Bx để diện tích ΔAIO có giá trị lớn nhất.

Hướng dẫn giải

a) Vì I là trung điểm của AN ⇒ OI ⊥ AN ( đường kính đi qua trung điểm của dây thì vuông góc với dây đó)

Ta lại có: 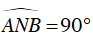 ( góc nội tiếp chắn nửa đường tròn)

Do Bx là tiếp tuyến với (O) tại B nên 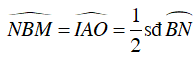 (góc tạo bởi tia tiếp tuyến với dây cung và góc nội tiếp cùng chắn cung BN).

Xét ΔAIO và ΔBMN , có:

⇒ ΔAIO ∼ ΔBMN (g.g)

Gọi K là trung điểm của OM

Vì 

⇒ ΔOIM vuông tại I 

Và ΔOBM vuông tại B 

⇒ IK = OK = MK = BK

nên các điểm B, O, I, M cùng thuộc đường tròn đường kính MO,

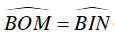
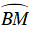
suy ra  ( hai góc nội tiếp cùng chắn  )

Xét ΔOBM và ΔINB có:

 (cmt)

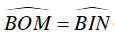
Suy ra ΔOBM ∼ ΔINB (g.g)

b) Kẻ IH ⊥ AO ta có: S_ΔAIO = 1/2 AO.IH

Vì AO không đổi nên S_ΔAIO lớn nhất ⇔ IH lớn nhất.

Xét ΔAOI vuông tại I, gọi E là trung điểm của OA

Khi đó: 

⇒ I thuộc đường tròn tâm E bán kinh 

Mà O, A cố định nên khi M chuyển động trên tia Bx thì I chạy trên nửa đường tròn đường kính AO

Do đó IH lớn nhất khi IH là bán kính của đường tròn tâm E, bán kính  .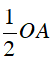

Suy ra H trùng E hay H là trung điểm của OA

Xét ΔAIO vuông tại I: có IH vừa là đường cao vừa là đường trung tuyến

Nên ΔAIO vuông cân tại I

 (hai góc ở đáy).

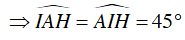
Suy ra ΔABM vuông cân tại B nên BM = BA = 2R

Vậy khi M thuộc Bx sao cho BM = 2R thì S_ΔAIO lớn nhất.

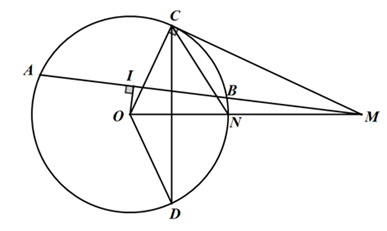
Ví dụ 3 : Cho đường tròn (O; R) và dây AB, gọi I là trung điểm của dây AB. Trên tia dối của tia BA lấy điểm M. Kẻ hai tiếp tuyến MC, MD với đường tròn, (C,D ≠ (O)) .

a) Chứng minh rằng: Năm điểm O, I, C, M, D cùng nằm trên một đường tròn.

b) Gọi N là giao điểm của tia OM với (O). Chứng minh rằng N là tâm đường tròn nội tiếp của ΔCMD.

Hướng dẫn giải

a) Vì MC, MD là các tiếp tuyến tại C, D với đường tròn (O) nên 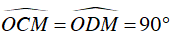 (1)

Mặt khác I là trung điểm của dây AB nên OI ⊥ AB hay 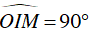 (2)

Từ (1), (2) suy ra 5 điểm M, C, D, O, I cùng thuộc đường tròn đường kính OM.

b) Vì MC, MD là các tiếp tuyến của (O) nên MO là phân giác của 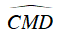 (3) và OM là phân giác của 

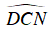
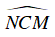
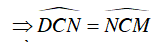
Ta có:  là góc nội tiếp chắn 

 là góc tạo bởi tia tiếp tuyến và dây cung chắn 

 ( góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn hai cung bằng nhau)

Suy ra CN là phân giác của 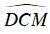 (4)

Từ (3) và (4) suy ra N là giao điểm các đường phân giác trong của ΔCMD hay N là tâm đường tròn nội tiếp ΔCMD.

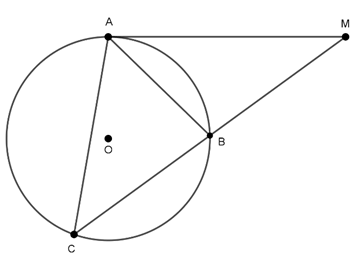
Ví dụ 4 : Từ điểm M nằm ngoài đường tròn (O) vẽ hai tiếp tuyến MA, MB với (O) tại A và B. Qua A vẽ đường thẳng song song với MB cắt đường tròn tại C. Nối C với M cắt đường tròn (O) tại D.Nối A với D cắt MB tại E. Chứng minh rằng:

a) ΔABE ∼ ΔBDE; ΔMEA ∼ ΔDEM.

b) E là trung điểm của MB.

Hướng dẫn giải

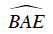
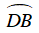
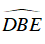
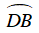
a) Ta có  là góc nội tiếp chắn cung  và  là góc tạo bởi tia tiếp tuyến và dây cung cùng chắn  .

⇒ 

Xét ΔABE và ΔBDE có:

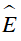
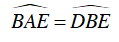
Góc  chung

 (cmt)

⇒ ΔABE ∼ ΔBDE (g.g)

Vì AC // MB nên 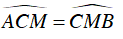 (hai góc so le trong)

Mà 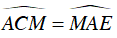 (góc nội tiếp và góc giữa tia tiếp tuyến và dây cung cùng chắn cung AD )

Suy ra: 

Xét ΔMEA và ΔDEM có:

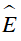
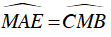
Góc  chung

 (cmt)

⇒ ΔMEA ∼ ΔDEM (g.g)

b) Theo chứng minh a) ta có:

ΔABE ∼ ΔBDE ⇒ AE/BE = BE/DE ⇒ EB² = AE.DE

ΔMEA ∼ ΔDEM ⇒ ME/DE = EA/EM ⇒ ME² = DE.EA

Do đó EB² = EM² hay EB = EM.

Vậy E là trung điểm của MB.

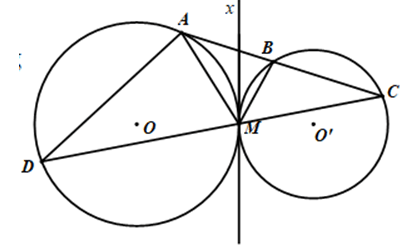
Ví dụ 5 : Cho hai đường tròn (O) và (O’) tiếp xúc ngoài với nhau tại M. Kẻ đường thẳng d tiếp xúc với (O) tại A và cắt (O’) tại B và C (B nằm giữa A và C)

Gọi D là giao điểm của CM và (O). Chứng minh rằng:

a) MA là phân giác của 

b) MA² = MB.MD

Hướng dẫn giải

a) Kẻ tiếp tuyến chung Mx của hai đường tròn (O) và (O’)

Ta có:

 (góc giữa tia tiếp tuyến và dây cung cùng chắn cung AM của (O)).

 (góc giữa tia tiếp tuyến và dây cung với góc nội tiếp cùng chắn cung MB của (O’)).

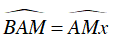
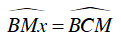
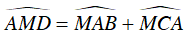
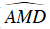
Mặt khác  (  là góc ngoài của tam giác AMC)

⇒ 

Vậy MA là phân giác của  .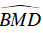

b) Xét ΔMAD và ΔMBA có:

 (cmt)

 ( góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung AM)

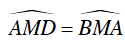
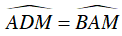
⇒ ΔMAD ∼ ΔMBA (g.g)

⇒ MA/MB = MD/MA hay MA² = MB.MD

C. Bài tập trắc nghiệm

Câu 1 : Kết luận nào sau đây là đúng

A. Trong một đường tròn, góc tạo bởi tia tiếp tuyến và dây cung có số đo lớn hơn góc nội tiếp chắn cung đó

B. Trong một đường tròn, góc tạo bởi tia tiếp tuyến và dây cung có số đo nhỏ hơn góc nội tiếp chắn cung đó

C. Trong một đường tròn, góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn một cung thì bằng nhau

D. Trong một đường tròn, góc tạo bởi tia tiếp tuyến và dây cung có số đo bằng hai lần số đo của góc nội tiếp chắn cung đó

Hướng dẫn giải

Đáp án C

Trong một đường tròn, góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn một cung thì bằng nhau.

Câu 2 : Cho đường tròn (O; R) có dây BC không phải đường kính. Dựng hai tiếp tuyến tại B và C chúng cắt nhau tại A. Biết rằng 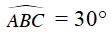 . Tính BC theo R?

A. BC = 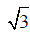 R

B. BC = 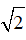 R

C. BC = R

D. Đáp án khác

Hướng dẫn giải

Đáp án C

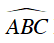
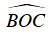
Ta lại có:  là góc tạo bởi tia tiếp tuyến và dây cung chắn 

 là góc ở tâm chắn 

⇒ 

Xét tam giác OBC, có OB = OC nên suy ra tam giác OBC cân tại O

Mà 

⇒ ΔOBC đều

⇒ OB = BC = OC = R.

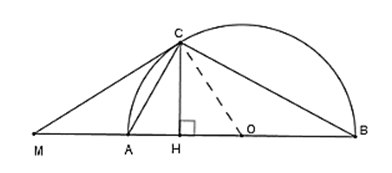
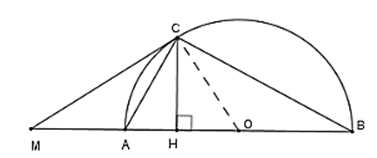
Câu 3 : Cho nửa đường tròn (O) đường kính AB. Trên tia đối AB lấy điểm M. Vẽ tiếp tuyến MC với nửa đường tròn . Gọi H là hình chiếu của C trên AB. CA là tia phân giác của góc nào dưới đây?

Hướng dẫn giải

Đáp án B

Xét nửa đường tròn tâm O có 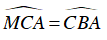 (*) (góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung AC).

Lại có 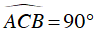 (góc nội tiếp chắn nửa đường tròn)

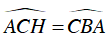
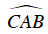
Suy ra:  (**) (cùng phụ với góc  )

Từ (*) và (**) ta có: 

Nên CA là tia phân giác của góc  .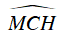

Câu 4 : Cho nửa đường tròn (O) đường kính AB. Trên tia đối AB lấy điểm M. Vẽ tiếp tuyến MC với nửa đường tròn . Gọi H là hình chiếu của C trên AB. Giả sử OA = a; MC = 2a . Độ dài CH.

Hướng dẫn giải

Đáp án C

Ta có OA = OC = a

Xét tam giác vuông MCO vuông tại C (do MC là tiếp tuyến của đường tròn O)

Xét tam giác MCO, có:

Vậy  .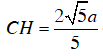

Câu 5 : Cho đường tròn tâm (O), điểm M nằm ngoài đường tròn. Qua M dựng tiếp tuyến MA đến đường tròn (O), dựng cát tuyến MBC (B nằm giữa B và C). Đẳng thức nào sau đây đúng.

A. MA² = MB.MC

B. MB² = MA.MC

C. MC² = MA.MB

D. 

Hướng dẫn giải

Đáp án A

Xét ΔMAB và ΔMCA , ta có:

 : Chung

 (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung AB)

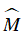
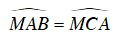
⇒ ΔMAB ∼ ΔMCA (g – g)

 .

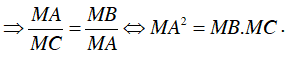
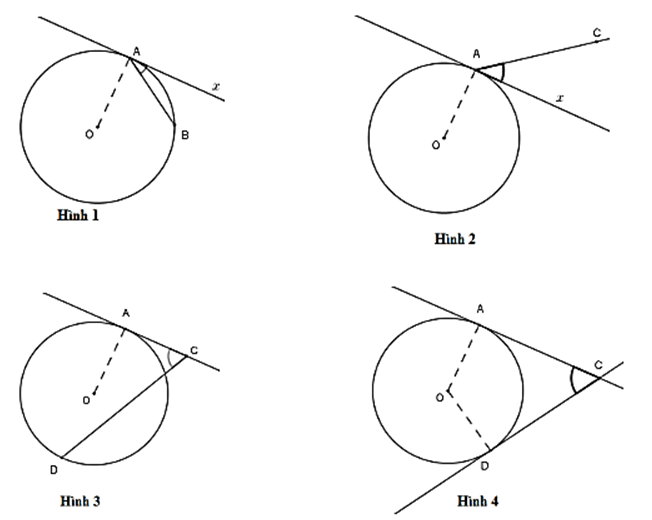
Câu 6 : Góc ở hình nào dưới đây biểu diễn góc tạo bởi tiếp tuyến và dây cung

A. Hình 1

B. Hình 2

C. Hình 3

D. Hình 4

Hướng dẫn giải

Đáp án A

Cho đường tròn tâm (O) có Ax là tia tiếp tuyến tại điểm A và dây cung AB. Khi đó góc BAx là góc tạo bởi tia tiếp tuyến và dây cung.

Câu 7 : Góc tạo bởi tiếp tuyến và dây cung có số đo bằng

A. 90^o

B. Số đo góc ở tâm chắn cung đó

C. Nửa số đo góc nội tiếp chắn cung đó

D. Nửa số đo cung bị chắn

Hướng dẫn giải

Đáp án D

Góc tạo bởi tiếp tuyến và dây cung có số đo bằng nửa số đo cung bị chắn.

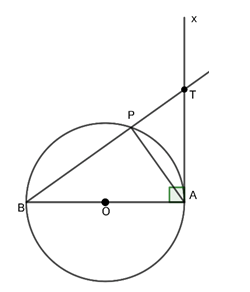
Câu 8 : Cho đường tròn tâm O, đường kính AB, dựng tiếp tuyến Ax với đường tròn. Lấy P là điểm bất kì trên đường tròn, BP cắt Ax tại T. Tìm khẳng định sai

Hướng dẫn giải

Đáp án B

Ta có 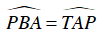 (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung PA). Suy ra D đúng.

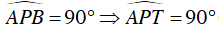
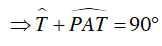
Ta lại có:  ( góc nội tiếp chắn nửa đường tròn tâm O)

 (hai góc phụ nhau)

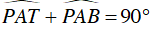
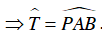
Mà  (hai góc phụ nhau)

 . Suy ra A đúng.

Tam giác OPA có OP = OA nên tam giác OPA cân tại O nên 

 . Nên C đúng

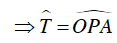
Vậy B sai.

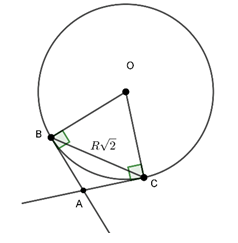
Câu 9 : Cho đường tròn (O) và dây BC = 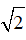 R. Hai tiếp tuyến của đường tròn (O) tại B và C cắt nhau tại A. Tính góc 

A. 45^o

B. 30^o

C. 60^o

D. 75^o

Hướng dẫn giải

Đáp án A

Ta có 

Và

Nên tam giác OBC vuông cân tại O

Mà