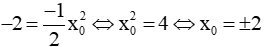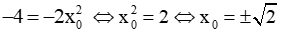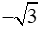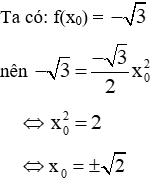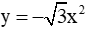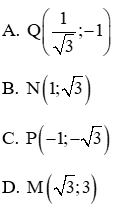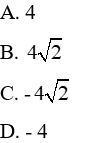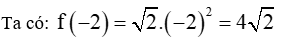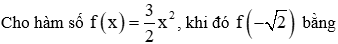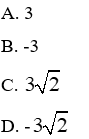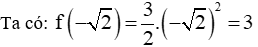Tính giá trị của hàm số bậc hai tại 1 điểm hay, chi tiết

A. Phương pháp giải

Cho hàm số y = f(x) = ax²

- Để tính giá trị của hàm số tại x = x₀ ta thay x bởi x₀ trong biểu thức ax²

- Nếu biết f(x₀) = b để tính x₀ ta giải phương trình

- Để kiểm tra điểm M(x₀;y₀) có thuộc đồ thị hàm số y = ax² ta thay tọa độ của M        vào công thức y = ax² nếu được đẳng thức đúng thì điểm M thuộc đồ thị hàm số , nếu được đẳng thức sai thì điểm M không thuộc đồ thị hàm số

Ví dụ 1: Cho hàm số 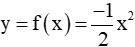 , tìm x₀ để f(x₀) = -2

Giải:

Ta xét phương trình 

Ví dụ 2: Cho hàm số f(x) = 2x², tính giá trị của hàm số tại x₀ = 1

Giải:

Giá trị của hàm số tại x₀ = 1 là: f(1) = 2.(1)² = 2

Ví dụ 3: Cho hàm số f(x) = 3x², hãy cho biết các điểm sau đây có thuộc đồ thị của hàm số không ?

a. M(-1;3)

b. N(2;4)

Giải:

a. Thay tọa độ điểm M(-1;3) vào công thức của hàm số f(x) = 3x² ta được:

3 = 3.(-1)² ⇔  3 = 3 (đúng)

Vậy điểm M thuộc đồ thị của hàm số

b. Thay tọa độ điểm N(2;4) vào công thức của hàm số f(x) = 3x² ta được:

4 = 3.(2)² ⇔  4 = 12 (sai)

Vậy điểm N không thuộc đồ thị của hàm số

B. Bài tập

Câu 1: Cho hàm số f(x) = -2x², f(x₀) = -4. Tính x₀

Giải

Ta có f(x₀) = -4 nên:  

Vậy đáp án là A

Câu 2: Cho hàm số f(x) = x², f(x₀) = -1. Tính x₀

Giải

Ta có f(x₀) = -1 nên -1 = x₀² ( vô nghiệm )

Vậy đáp án là D

Câu 3: Cho hàm số , điểm nào sau đây không thuộc đồ thị hàm số

A. M(0;0)

B. N(1;-1)

C. P(-1;-1)

D. Q(-2;4)

Giải

Thay tọa độ của điểm M vào công thức hàm số y = -x²

Ta được: 0 = 0 (đúng) ⇒ điểm M thuộc đồ thị hàm số

Thay tọa độ của điểm N vào công thức hàm số y = -x²

Ta được: -1 = -1 (đúng) ⇒ điểm N thuộc đồ thị hàm số

Thay tọa độ của điểm P vào công thức hàm số y = -x²

Ta được: -1 = -1 (đúng) ⇒ điểm P thuộc đồ thị hàm số

Thay tọa độ của điểm Q vào công thức hàm số y = -x²

Ta được: 4 = -4 (sai) ⇒ điểm Q không thuộc đồ thị hàm số

Vậy đáp án là D

Câu 4: Cho hàm số 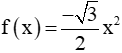 , tìm hoành độ điểm thuộc đồ thị hàm số biết tung độ của điểm đó là 

Giải

Vậy đáp án là D

Câu 5: Cho hàm số 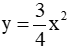, điểm nào sau đây thuộc đồ thị hàm số

A. M(-2;3)

B. N(1;3)

C. P(-1;3)

D. Q(0;1)

Giải

Thay tọa độ của điểm M vào công thức hàm số

Ta được: 3 = 3 (đúng) ⇒ điểm M thuộc đồ thị hàm số

Thay tọa độ của điểm N vào công thức hàm số

Ta được: 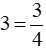 (sai) ⇒ điểm N không thuộc đồ thị hàm số

Thay tọa độ của điểm P vào công thức hàm số

Ta được: 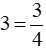 (sai) ⇒ điểm P không thuộc đồ thị hàm số

Thay tọa độ của điểm Q vào công thức hàm số

Ta được: 1 = 0 (sai) ⇒ điểm Q không thuộc đồ thị hàm số

Vậy đáp án là A

Câu 6: Cho hàm số 

Giải

Thay tọa độ của điểm Q vào công thức hàm số

Ta được: 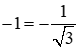  (sai) ⇒ điểm Q không thuộc đồ thị hàm số

Thay tọa độ của điểm N vào công thức hàm số

Ta được: 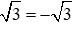 (sai) ⇒ điểm N không thuộc đồ thị hàm số

Thay tọa độ của điểm P vào công thức hàm số

Ta được: 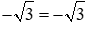 (đúng) ⇒ điểm P thuộc đồ thị hàm số

Thay tọa độ của điểm M vào công thức hàm số

Ta được: 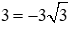  (sai) ⇒ điểm M không thuộc đồ thị hàm số

Vậy đáp án là C

Câu 7: Cho hàm số 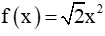, khi đó f(-2) bằng

Giải

Vậy đáp án là B

Câu 8: 

Giải

Vậy đáp án là A

Câu 9: Cho hàm số f(x) = 5x², tính tung độ của điểm thuộc đồ thị hàm số biết hoành độ của điểm đó bằng 0

A. 1

B. -5

C.  0

D. 5

Giải

Ta có: f(0) = 5.(0)² = 0

Vậy đáp án là C