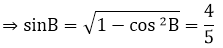Vị trí tương đối của hai đường tròn hay, chi tiết

Lý thuyết và Phương pháp giải

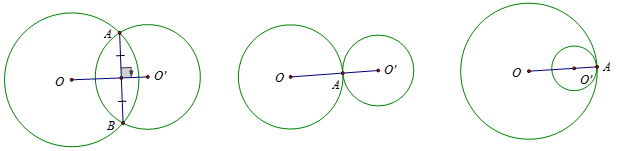
1. Bảng tóm tắt

2. Tính chất đường nối tâm

    Đường nối tâm là trục đối xứng của hình gồm cả đường tròn

    - Nếu hai đường tròn cắt nhau thì đường nối tâm là đường trung trực của dây chung

    - Nếu hai đường tròn tiếp xúc nhau thì tiếp điểm nằm trên đường nối tâm

Ví dụ minh họa

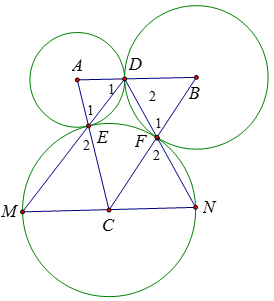
Ví dụ 1: Cho các đường tròn (A; 9); (B; 16); (C; 20) tiếp xúc ngoài với nhau từng đôi một. Đường tròn (A) tiếp xúc với đường tròn (B) và (C) lần lượt tại D và E. Đường tròn (B) và (C) tiếp xúc với nhau tại F. Hai tia DE và DF cắt đường tròn (C) tại M và N

    a) Chứng minh rằng MN // AB

    b) Tính diện tích tam giác ABC

Hướng dẫn:

    a) Các đường tròn (A), (B), (C) tiếp xúc ngoài nên ba điểm A, D, B thẳng hàng; ba điểm A, E, C thẳng hàng; B, F, C thẳng hàng.

    Nối CM, CN ta có:

    ⇒ CM // AB ; CN // AB

    Do đó theo tiên đề Ơ-clit thì C, M, N thẳng hàng

    Vậy MN // AB

    b) Xét tam giác ABC có:

    AB = AD + DB = 9 + 16 = 25

    BC = BF + FC = 16 + 20 = 36

    CA = CE + EA = 20 + 9 = 29

    Áp dụng định lí cosin, ta có:

    AC² = AB² + BC² - 2AB.BC.cosB

    ⇒ 29² = 25² + 36² - 2.25.36.cosB

    ⇒ cosB = 3/5

    Diện tích tam giác ABC là:

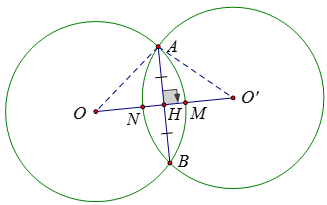
Ví dụ 2: Cho hai đường tròn (O) và (O’) có cùng bán kính R cắt nhau tại A và B. Đoạn nối tâm OO’ cắt đường tròn (O) và (O’) lần lượt tại M và N. Cho biết MN = 6cm ; AB = 12 cm.

    a) Chứng minh rằng ON = O’M

    b) Tính độ dài đoạn nối tâm

Hướng dẫn:

    a) Ta có: ON = OO’ – O’N = OO’ – R

    O’M = OO’ – OM = OO’ – R

    ⇒ ON = O’M (1)

    b) Gọi H là giao điểm của OO’ và AB

    Ta có: OO'⊥ AB và HA = HB = 6 cm

    ΔOAO’ cân tại A có AH là đường cao nên cũng là trung tuyến

    ⇒ OH = O’H (2)

    Từ (1) và (2) ⇒ H là trung điểm của MN ⇒ HN = HM = 3cm

    Xét ΔOAH vuông tại H, có: OA² = AH² + OH²

    ⇒ R² = 6² + (R - 3)² ⇒ R = 7,5 cm

    OH = OM – HM = 7,5 – 3 = 4,5 cm

    Do đó: OO’ = 2OH = 9 cm

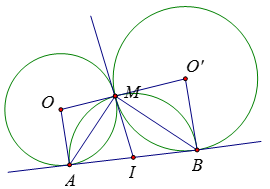
Ví dụ 3: Cho hai điểm A, B. Hai đường tròn thay đổi tiếp xúc với AB lần lượt tại A và B và tiếp xúc nhau tại M

    Tìm tập hợp các điểm M

Hướng dẫn:

    a) Phần thuận

    Kẻ tiếp tuyến chung qua M của (O), (O’) cắt AB tại I.

    Theo tính chất tiếp tuyến ta có: IA = IB = IM

    Vậy tập hợp điểm M là đường tròn (I; AB/2) với I là trung điểm của AB

    Giới hạn: M ≢ A,B

    b) Phần đảo

    Trên (I; AB/2) lấy điểm M’ bất kì. Gọi O₁ là giao điểm của đường vuông góc với AB tại A và đường trung trực của M’A; vẽ đường tròn (O₁,O₁ A). Tương tự vẽ đường tròn (O₂, O₂B) rồi chứng minh hai đường tròn (O₁,O₁ A) và (O₂,O₂ B) tiếp xúc nhau tại M. Dễ dàng chứng minh được O₁, M, O₂ thẳng hàng và O₁ O₂ = O₁ M+MO₂. Như vậy đường nối tâm bằng tổng hai bán kính nên (O₁,O₁ A) và (O₂,O₂ B) tiếp xúc nhau tại M

    Vậy quỹ tích những điểm M là đường tròn đường kính AB (không kể A và B)