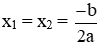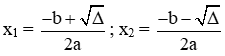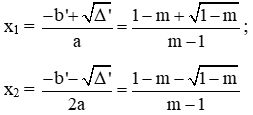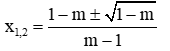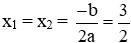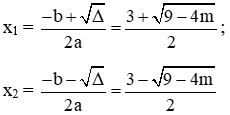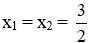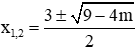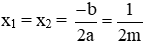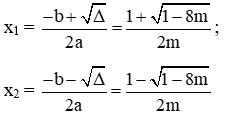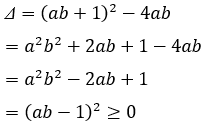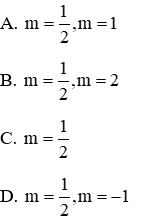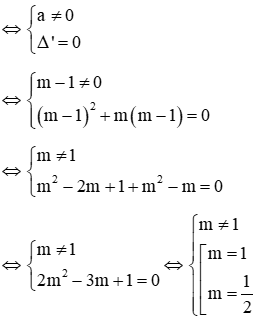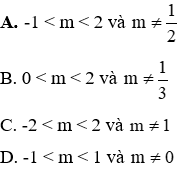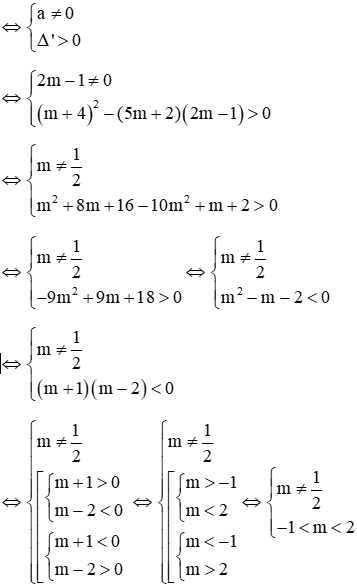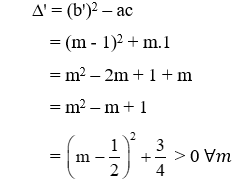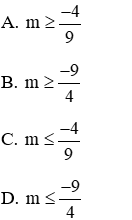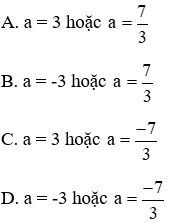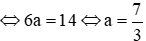Cách giải và biện luận phương trình bậc hai một ẩn cực hay

A. Phương pháp giải

B₁: Nếu phương trình chưa ở dạng ax² + bx + c = 0 thì biến đổi đưa phương trình về đúng dạng này

B₂: Nếu hệ số a chứa tham số ta xét 2 trường hợp

- Trường hợp 1: a = 0, ta giải và biện luận phương trình bx + c = 0

- Trường hợp 2: a  ≠ 0, ta lập biểu thức ∆ = b² – 4ac. Khi đó:

+ Nếu ∆ < 0 thì phương trình vô nghiệm

+ Nếu ∆ = 0 thì phương trình có nghiệm kép:  

+ Nếu ∆ > 0 thì phương trình có 2 nghiệm phân biệt:

B₃: Kết luận

Ví dụ 1: Giải và biện luận phương trình mx² – 2x + m = x² – 2mx

Giải

Phương trình đã cho ⇔ mx² - 2x + m - x² + 2mx = 0

⇔ (m - 1)x² + 2(m - 1)x + m = 0 (1)

Trường hợp 1: m = 1 thì phương trình (1) trở thành: 1 = 0 (phương trình vô nghiệm)

Trường hợp 2: m ≠ 1 thì phương trình (1) là phương trình bậc hai có

∆ꞌ = (bꞌ)² – ac = (m-1)² – (m-1).(m) = m² – 2m + 1 - m² + m = 1 - m

+ Nếu ∆ꞌ < 0 ⇔ 1 - m < 0 ⇔ m > 1  thì phương trình vô nghiệm

+ Nếu ∆ꞌ = 0 ⇔ 1 - m = 0 ⇔ m = 1 (loại vì m ≠ 1)

+ Nếu ∆ꞌ  > 0 ⇔ 1 - m > 0 ⇔ m < 1 thì phương trình có 2 nghiệm phân biệt:

Kết luận : - Nếu m ≥ 1 thì phương trình vô nghiệm

- Nếu m < 1 thì phương trình có hai nghiệm phân biệt:

Ví dụ 2: Giải và biện luận phương trình: x² – 3x + m = 0

Giải

Phương trình đã cho là phương trình bậc 2 có hệ số a = 1

Ta có: ∆ = b² – 4ac = (-3)² – 4.1.m = 9 – 4m

+ Nếu ∆ < 0 ⇔ 9 - 4m < 0 ⇔ 4m > 9 ⇔ m > 9/4   thì phương trình vô nghiệm

+ Nếu ∆ = 0 ⇔ 9 - 4m = 0 ⇔ 4m = 9 ⇔ m = 9/4  thì phương trình có nghiệm kép:  

+ Nếu ∆ > 0 ⇔ 9 - 4m > 0 ⇔ 4m < 9 ⇔ m < 9/4 thì phương trình có 2 nghiệm phân biệt:

Kết luận :

- Nếu 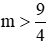 thì phương trình vô nghiệm

- Nếu 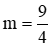 thì phương trình có nghiệm kép 

- Nếu 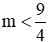 thì phương trình có hai nghiệm phân biệt 

Ví dụ 3: Giải và biện luận phương trình  mx² – x + 2 = 0(1)

Giải

Trường hợp 1: nếu m = 0 thì phương trình (1) trở thành

-x + 2 = 0 ⇔ x = 2

Trường hợp 2: nếu m ≠ 0 thì phương trình (1) là phương trình bậc hai có:

∆ = b² – 4ac = (-1)² – 4.2.m = 1 – 8m

+ Nếu ∆ < 0 ⇔ 1 - 8m < 0 ⇔ 8m > 1 ⇔ m > 1/8  thì phương trình vô nghiệm

+ Nếu ∆ = 0 ⇔ 1 - 8m = 0 ⇔ 8m = 1 ⇔ m = 1/8 thì phương trình có nghiệm kép: 

+ Nếu ∆ > 0 ⇔ 1 - 8m > 0 ⇔ 8m < 1 ⇔ m < 1/8 thì phương trình có 2 nghiệm phân biệt:

Kết luận:

B. Bài tập

Câu 1: Tìm m để phương trình x² – mx - x + m = mx – 3m (1) có nghiệm kép

A. m = 1

B. m = 2

C. m = 3

D. m = 4

Giải

Phương trình (1) ⇔ x² - mx - x + m - mx + 3m = 0

⇔ x² - 2(m + 1) + 4m = 0

Phương trình (1) là phương trình bậc hai có

∆ꞌ = (bꞌ)² – ac = (m+1)² - 4m.1

= m² + 2m + 1 - 4m

= m² – 2m + 1 =

Suy ra phương trình  (1) có nghiệm kép khi  ∆ꞌ = 0 ⇔ (m - 1)² = 0 ⇔ m = 1

Vậy đáp án đúng là A

Câu 2: Tìm a và b để phương trình ax² + (ab + 1)x + b = 0 (1) vô nghiệm

A. a = 2, b = -4

B. a = 1, b ∈ R

C. a > 0, b < 1

D. Không có giá trị nào của a và b

Giải

Nếu a = 0 thì phương trình (1) có dạng x + b = 0 ⇔ x = -b

⇒ với a = 0 và b ∈ R thì (1) luôn có một nghiệm (loại)

Nếu a ≠ 0 thì (1) là phương trình bậc hai có

phương trình (1) luôn có nghiệm với mọi a, b (loại)

Vậy không có giá trị nào của a và b để phương trình (1) vô nghiệm

Đáp án D

Câu 3: Tìm m để phương trình (m – 1)x² – 2mx + m + 1 = 0 (1) vô nghiệm

A. m > -3

B. m = -2

C. m < 7

D. Không có giá trị nào của m

Giải

Trường hợp 1: nếu m = 1 thì phương trình (1) trở thành

⇔ -2x + 2 = 0 ⇔ x = 1 ⇔  m = 1 (không thỏa mãn)

Trường hợp 2: nếu m ≠ 1 thì phương trình (1) là phương trình bậc hai có

∆ꞌ = (bꞌ)² – ac = m² – (m – 1)(m + 1) = m² – m² + 1 = 1 > 0 ∀ m ≠ 1

Suy ra phương trình  (1) luôn có nghiệm với mọi m, nghĩa là không có giá trị nào của m để phương trình vô nghiệm

Vậy đáp án đúng là D

Câu 4: Tìm m để phương trình mx² + 2mx + m - 4 = 0 (1) có ít nhất một nghiệm

A. m > 0

B. m < 0

C. m < 1

D. m > 1

Giải

Trường hợp 1: nếu m = 0 thì phương trình (1) trở thành

-4 = 0 (phương trình vô nghiệm)

⇒ m = 0 (không thỏa mãn)

Trường hợp 2: nếu m ≠ 0 thì phương trình (1) là phương trình bậc hai có

∆ꞌ = (bꞌ)² – ac = m² –m(m – 4) = m² – m² + 4m = 4m

Để phương trình (1) có ít nhất một nghiệm thì  ∆ꞌ ≥ 0 ⇔ 4m ≥ 0 ⇔ m ≥ 0

Vì đang xét m ≠ 0 nên m > 0

Vậy với m > 0 thì phương trình có ít nhất 1 nghiệm

Vậy đáp án đúng là A

Câu 5: Tìm m để phương trình (m - 1)x² + 2(m - 1)x - m = 0 (1) có nghiệm kép

Giải

Phương trình (1) có nghiệm kép

Với m = 1, không thỏa mãn m ≠ 1 nên loại

Với 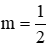, thỏa mãn m ≠ 1nên nhận

Vậy với 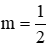 thì phương trình có nghiệm kép.

Đáp án đúng là C

Câu 6: Tìm m để phương trình (2m-1)x² - 2(m + 4)x +5m + 2 = 0 (1) có 2 nghiệm phân biệt

Giải

Phương trình (1) có nghiệm 2 nghiệm phân biệt

Vậy với -1 < m < 2 và 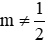 thì phương trình có 2 nghiệm phân biệt

Đáp án là A

Câu 7: Tìm m để phương trình x² – 2(m - 1)x – m = 0(1) có hai nghiệm phân biệt

A. m > 1

B. m = 2

C. m < 2

D. ∀ m ∈ R

Giải

Phương trình (1) là phương trình bậc hai có

Suy ra phương trình  (1) luôn có 2 nghiệm phân biệt

Vậy đáp án đúng là D

Câu 8: Tìm m để phương trình (m + 2)x² – (2m + 3)x + m = 0(1) có nghiệm

Giải

Trường hợp 1: nếu m = -2 thì phương trình (1) trở thành

x - 2 = 0 ⇔ x = 2 ⇒ m = -2 (thỏa mãn)

Trường hợp 2: nếu m ≠ -2 thì phương trình (1) là phương trình bậc hai có

∆ = b² – 4ac = (2m + 3)² – 4m(m + 2) = 4m + 9

Phương trình (1) có nghiệm ⇔ Δ ≥ 0 ⇔ 4m + 9 ≥ 0 ⇔ m ≥ 

Kết hợp 2 trường hợp ta có  với m ≥ 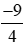 thì phương trình (1) có nghiệm     

Vậy đáp án đúng là B

Câu 9: Tìm a để phương trình (a – 3)x² – 2(a - 1)x + a - 5 = 0(1) có một nghiệm

Giải

Trường hợp 1: nếu a = 3 thì phương trình (1) trở thành

-4x - 2 = 0 ⇔ x = 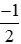 ⇒  a = 3 (thỏa mãn)

Trường hợp 2: nếu a ≠ 3 thì phương trình (1) là phương trình bậc hai có

∆ꞌ = (bꞌ)² – ac = (a - 1)² – (a - 3)(a - 5) = a² - 2a + 1 – a² + 8a – 15 = 6a – 14

Suy ra phương trình  (1) có 1 nghiệm khi 6a – 14 = 0 

Vậy với a = 3 hoặc 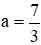 thì phương trình có 1 nghiệm

Vậy đáp án đúng là A

Câu 10: Tìm m để phương trình x² – 2mx – m² – 1 = 0 có hai nghiệm phân biệt

A. m > 0

B. Mọi giá trị của m

C. m < 7

D. Không có giá trị nào của m

Giải

Phương trình có hai nghiệm phân biệt ⇔ Δ' > 0 

⇔ m² - 1.(-m² - 1) > 0

⇔ 2m² + 1 > 0 luôn đúng với mọi m

Vậy phương trình đã cho luôn có hai nghiệm phân biệt với mọi m

Đáp án B