Cách biện luận số giao điểm của đường thẳng và parabol cực hay, có đáp án

A. Phương pháp giải

Dạng 4.2.1. Biện luận số giao điểm của parabol và đường thẳng bằng phương pháp đại số:

Bước 1:Viết phương trình hoành độ giao điểm của parabol và đường thẳng.

Bước 2:Biện luận số giao điểm của parabol và đường thẳng theo số nghiệm của phương trình (số giao điểm của đường thẳng (d) và parabol (P) là số nghiệm của phương trình hoành độ giao điểm).

+) (d) cắt (P) tại hai điểm phân biệt ((d) và (P) có hai điểm chung phân biệt) ⇒ phương trình hoành độ giao điểm có hai nghiệm phân biệt (Δ > 0 hoặc Δ < 0).

+) (d) tiếp xúc với (P) ((d) và (P) có một điểm chung) phương trình hoành độ giao điểm có nghiệm kép ( hoặc ).

+) (d) và (P) không cắt nhau phương trình hoành độ giao điểm vô nghiệm (Δ = 0 hoặc Δ' = 0).

Bước 3: Kết luận.

Dạng 4.2.2. Biện luận số giao điểm của parabol và đường thẳng bằng phương pháp hình học:

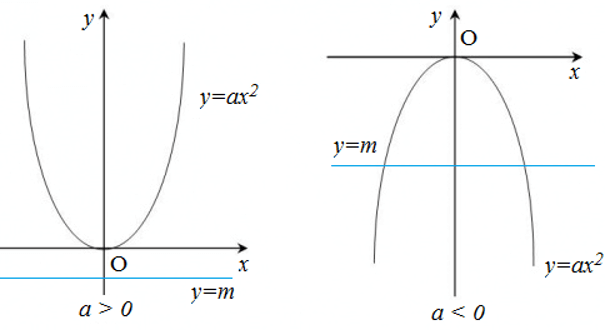
Trường hợp đường thẳng cho trước là đường thẳng (d): y = m(m ≠ 0) song song với trục hoành Ox.

Bước 1:Quan sát và biện luận số giao điểm dựa vào đồ thị của parabol và đường thẳng.

- Trường hợp 1: Nếu hàm số y = ax² có hệ số a > 0 thì đồ thị là đường cong parabol (P) nằm phía trên trục hoành Ox. Do đó,

+) Nếu m > 0 thì (d) cắt (P) tại hai điểm phân biệt.

+) Nếu m = 0 thì (d) tiếp xúc với (P).

+) Nếu m < 0 thì (d) và (P) không có điểm chung.

- Trường hợp 2: Nếu hàm số y = ax² có hệ số a < 0 thì đồ thị là đường cong parabol (P) nằm phía dưới trục hoành Ox. Do đó,

+) Nếu m < 0 thì (d) cắt (P) tại hai điểm phân biệt.

+) Nếu m = 0 thì (d) tiếp xúc với (P).

+) Nếu m > 0 thì (d) và (P) không có điểm chung.

Bước 2: Kết luận.

B. Các ví dụ điển hình

Ví dụ 1:Cho parabol (P): y = -3x² và các đường thẳng (d₁): y = 4x + 1, (d₂): y = x + 1, (d₃): y = -6x + 3. Số giao điểm của (P) với (d₁), (d₂), (d₃) lần lượt là:

Lời giải

Chọn D

Ví dụ 2:Cho parabol (P): y = x² và đường thẳng (d): y = x + m (với m là tham số). Khẳng định nào sau đây là đúng?

Lời giải

Chọn D

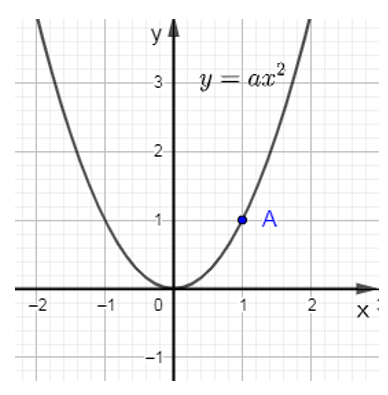
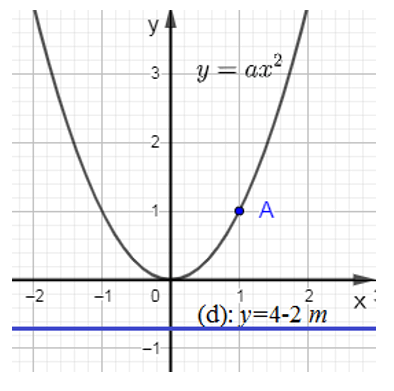
Ví dụ 3: Cho parabol (P): y = ax² (với a ≠ 0) có đồ thị như hình vẽ dưới đây. Số giao điểm của đường thẳng (d): y = 4 - 2m (với m là tham số) trong trường hợp m > 2 là:

Lời giải

Chọn A