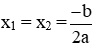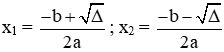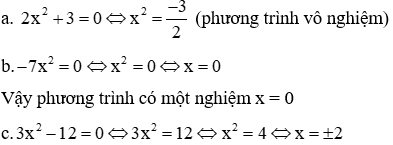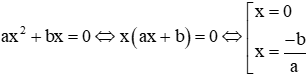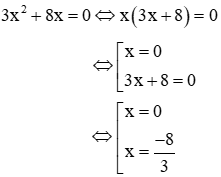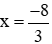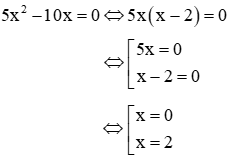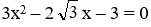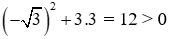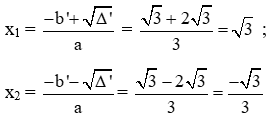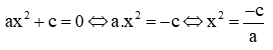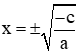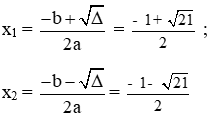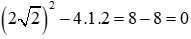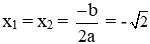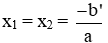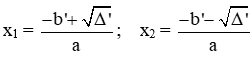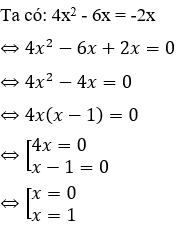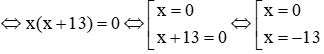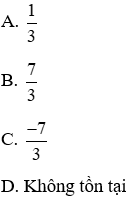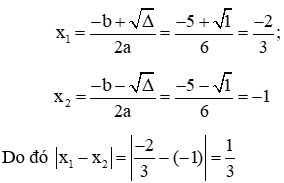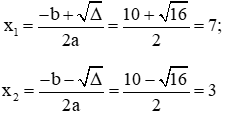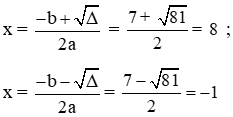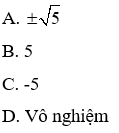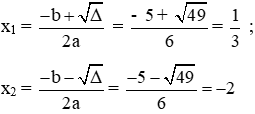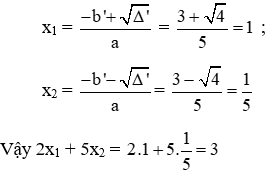Phương pháp giải phương trình bậc hai một ẩn hay, chi tiết

A. Phương pháp giải

Phương trình bậc hai một ẩn có dạng  ax² + bx + c = 0  (a ≠ 0). Để giải phương trình ta làm như sau

B₁: Xác định các hệ số a, b, c

B₂: Tính ∆ = b² - 4ac

+ Nếu ∆ < 0 thì phương trình vô nghiệm

+ Nếu ∆ = 0 thì phương trình có nghiệm kép:  

+ Nếu ∆ > 0 thì phương trình có 2 nghiệm phân biệt:

Ví dụ 1: Giải các phương trình sau:

a. 2x² + 3 = 0

b. -7x² = 0

c. 3x² – 12 = 0

Giải

Vậy phương trình có 2 nghiệm phân biệt: x = 2, x = -2

*Nếu hệ số c = 0 thì phương trình có dạng: ax² + bx = 0 (3)

Để giải phương trình (3) ngoài cách dùng  ∆ hoặc ∆ꞌ ở trên ta có thể làm như sau

Ví dụ 2: Giải các phương trình sau

a. 3x² +8x = 0

b. 5x² – 10x = 0

Giải

a. Ta có:

Vậy phương trình có 2 nghiệm là: x = 0, 

b. Ta có:

Vậy phương trình có 2 nghiệm là: x = 0, x = 2

Ví dụ 3: Giải phương trình x² + 3x + 3 = 0

Giải

Ta có: a = 1; b = 3; c = 3 ⇒ ∆ = b² – 4ac = 9 – 12 = - 3 < 0

Vậy phương trình vô nghiệm.

Ví dụ 4: Giải phương trình sau: 

Giải

Ta có: a = 3; bꞌ = -√3 ; c = -3 ⇒ ∆ꞌ = (bꞌ)² - ac = 

Vậy phương trình có hai nghiệm phân biệt:

* Nếu hệ số b = 0 thì phương trình có dạng: ax² + c = 0 (2)

Để giải phương trình (2) ngoài cách dùng  ∆ hoặc ∆ꞌ ở trên ta có thể làm như sau:

+ Nếu ac > 0 thì phương trình vô nghiệm

+ Nếu ac = 0 thì phương trình có nghiệm kép x = 0

+ Nếu ac < 0 thì phương trình có 2 nghiệm phân biệt

Ví dụ 5: Giải phương trình  x² + x - 5 = 0

Giải

Ta có: a = 1; b = 1; c = - 5 ⇒ ∆ = b² – 4ac = 1 + 20 = 21 > 0

Vậy phương trình có hai nghiệm phân biệt:

Ví dụ 6: Giải phương trình x² + 2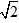x + 2 = 0

Giải

Ta có: a = 1; b = 2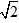; c = 2

⇒ ∆ = b² – 4ac = 

Vậy phương trình có nghiệm kép: 

* Công thức nghiệm thu gọn: Dùng khi hệ số b = 2bꞌ

Phương trình ax² + bx + c = 0 (a ≠ 0) có ∆ꞌ = (bꞌ)² - ac (b = 2bꞌ)

+ Nếu ∆ꞌ < 0 thì phương trình vô nghiệm

+ Nếu ∆ꞌ = 0 thì phương trình có nghiệm kép:  

+ Nếu ∆ꞌ > 0 thì phương trình có 2 nghiệm phân biệt

B. Bài tập

Câu 1: Số thực nào sau đây là nghiệm của phương trình x² - x + 8 = 0

A. 2

B. 10

C. -15

D. Không có

Giải

Ta có: a = 1; b = -1; c = 8 ⇒ ∆ = b² – 4ac = (-1)² – 4.1.8 = -31 <  0

Vậy phương trình vô nghiệm

Vậy đáp án đúng là D

Câu 2: Số nghiệm của phương trình  4x² - 6x = -2x là

A. 1                      

B. 0                   

C. 2                     

D. 3

Giải

Vậy đáp án đúng là C

Câu 3: Nghiệm của phương trình x² + 13x = 0 là

A. 13 và -13

B. 0 và -13

C. 0 và 13

D. Vô nghiệm

Giải

Phương trình x² + 13x = 0

Vậy đáp án đúng là B

Câu 4: Cho phương trình  2x² + 4x + 1 = -x² - x – 1. Tính |x₁ - x₂|

Giải

Phương trình 2x² + 4x + 1 = -x² - x – 1

Ta có: a = 3; b = 5; c = 2 ⇔ ∆ = b² – 4ac = (5)² – 4.3.2 = 1 >  0

⇒ Phương trình có hai nghiệm phân biệt

Vậy đáp án đúng là A

Câu 5: Cho phương trình x² - 10x + 21 = 0. Khẳng định nào sau đây đúng

A. Phương trình vô nghiệm

B. Phương trình có nghiệm không nguyên

C. Phương trình có 1 nghiệm

D. Phương trình có 2 nghiệm nguyên

Giải

Ta có: a = 1; b = -10; c = 21 ⇒ ∆ = b² – 4ac = (-10)² – 4.1.21 = 16 >  0

Phương trình có hai nghiệm phân biệt

Vậy đáp án đúng là D

Câu 6: Giả sử x₁ < x₂ là hai nghiệm của phương trình x² -7x - 8 = 0. Tính 2x₁

A. -2

B. 1

C. -1

D. 6

Giải

Ta có: a = 1; b = -7; c = -8 ⇒  ∆ = b² – 4ac = (-7)² – 4.1.(-8) = 81 >  0

Phương trình có hai nghiệm phân biệt

Suy ra x₁ = -1 do đó 2x₁ = -2

Vậy đáp án đúng là A

Câu 7: Nghiệm của phương trình 3x² + 15 = 0 là

Giải

Phương trình 3x² + 15 = 0 ⇔ 3x² = -15 ⇔ x² = -5 (vô nghiệm)

Vậy đáp án đúng là D

Câu 8: Một nghiệm của phương trình 3x² + 5x – 2 = 0 là

A. -2

B. -1

C. -5

D. 0

Giải

Ta có: a = 3; b = 5; c = -2 ⇒ ∆ = b² – 4ac = 5² – 4.3.(-2) = 49 > 0

Phương trình có hai nghiệm phân biệt:

Vậy đáp án đúng là A

Câu 9: Số nghiệm của phương trình 3x² - 6x + 3 = 0 là

A. 3

B. 2

C. 1                     

D. 0

Giải

Ta có: a = 3; bꞌ = -3; c = 3 ⇒ ∆ꞌ = (bꞌ)² - ac = (-3)² – 3.3 = 9 - 9 = 0

Suy ra phương trình có một nghiệm

Vậy đáp án đúng là C

Câu 10: Giả sử x₁, x₂ (x₁ > x₂) là hai nghiệm của phương trình 5x² - 6x + 1 = 0.      Tính 2x₁ + 5x₂

A. 6

B. 5

C. 4               

D. 3

Giải

Ta có: a = 5; bꞌ = -3; c = 1 ⇒ ∆ꞌ =(bꞌ)² - ac = (-3)² – 5.1 = 9 - 5 = 4 > 0

Suy ra phương trình có hai nghiệm phân biệt

Vậy đáp án đúng là D