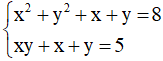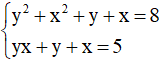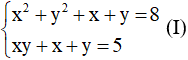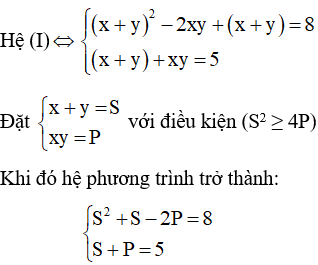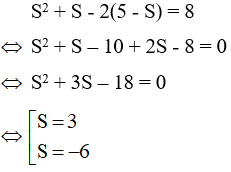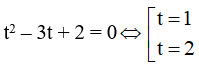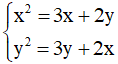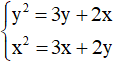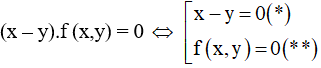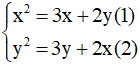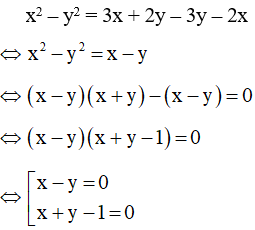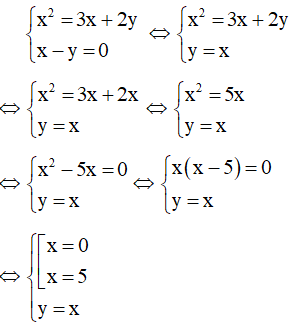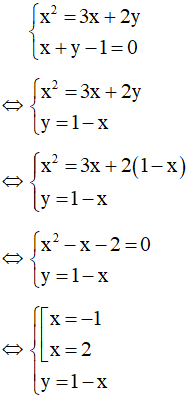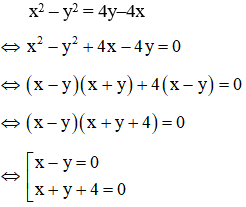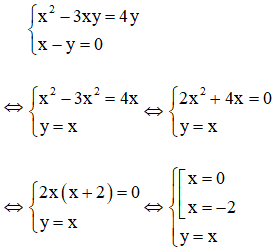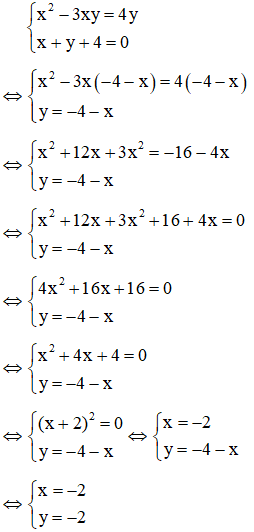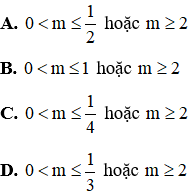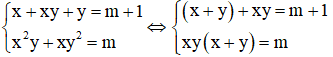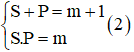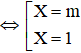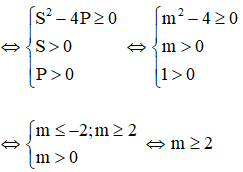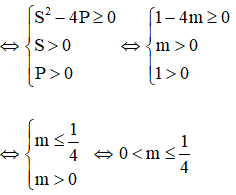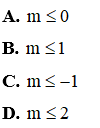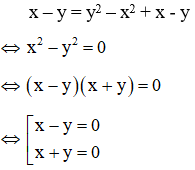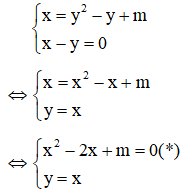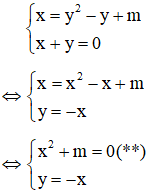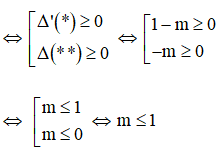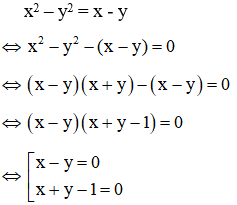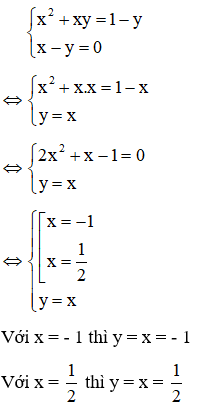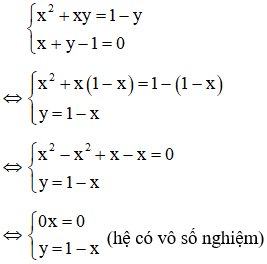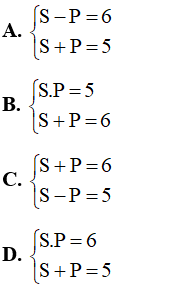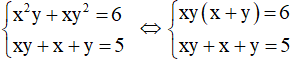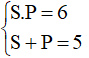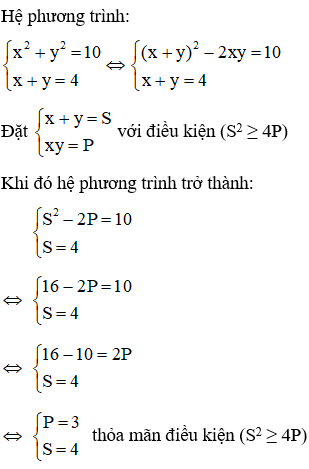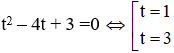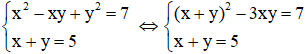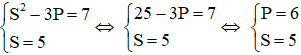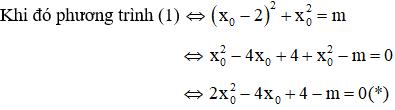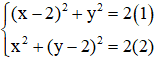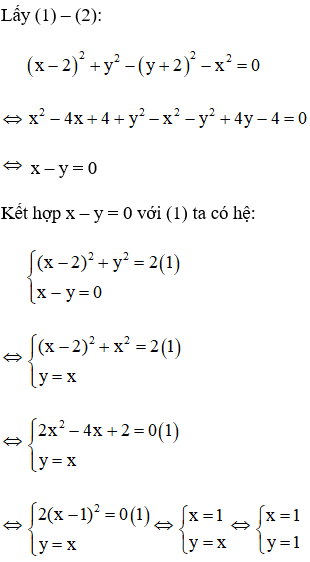Cách giải hệ phương trình đối xứng hai ẩn cực hay

A. Phương pháp giải

1. Hệ phương trình đối xứng loại 1

a. Dạng của hệ phương trình

- Là hệ gồm hai phương trình hai ẩn x, y mà khi thay x bởi y và thay y bởi x thì mỗi phương trình của hệ không thay đổi

- Ví dụ: Hệ phương trình 

Khi thay x bởi y và thay y bởi x thì được hệ 

Ta thấy mỗi phương trình của hệ không thay đổi nên hệ đã cho là hệ đối xứng loại 1

b. Cách giải

B1: Biến đổi biểu thức ở hai phương trình của hệ theo tổng và tích của x, y

B2: Đặt 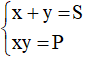 với điều kiện (S² ≥ 4P)

B3: Tìm S, P thỏa mãn điều kiện (S² ≥ 4P). Khi đó x, y là nghiệm của phương trình  t² – Sx + P = 0

B4: Kết luận

Ví dụ: giải hệ phương trình 

Giải

Từ S + P = 5 ⇒ P = 5 – S. Thế vào phương trình  S² + S -2P = 8 ta được

* Với S = 3 ⇒ P = 5 – 3 = 2 thỏa mãn điều kiện (S² ≥ 4P)

Ta có 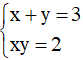, theo Vi-et x, y là nghiệm của phương trình:

Suy ra hệ có hai nghiệm: x = 1 và y = 2, x =2 và y = 1

* Với S = -6 ⇒ P = 5 – (-6) = 11 không  thỏa mãn điều kiện (S² ≥ 4P) nên loại

Vậy hệ đã cho có hai nghiệm: x = 1 và y = 2, x =2 và y = 1

2. Hệ phương trình đối xứng loại 2

a. Dạng của hệ phương trình

- Là hệ gồm hai phương trình hai ẩn x, y mà khi thay x bởi y và thay y bởi x thì  phương trình này trở thành phương trình kia và ngược lại nhưng hệ không thay đổi

- Ví dụ: Hệ phương trình 

Khi thay x bởi y và thay y bởi x thì được hệ 

Ta thấy phương trình này trở thành phương trình kia và ngược lại nhưng hệ không thay đổi nên hệ đã cho là hệ phương trình đối xứng loại 2

b. Cách giải

- B1: Trừ vế với vế của hai phương trình cho nhau ta được phương trình dạng

-B2: Kết hợp (*) với 1 phương trình của hệ, kết hợp (**) với 1 phương trình của hệ ta được hai hệ phương trình. Giải hai hệ phương trình đó

-B3: Kết luận

Ví dụ: giải hệ phương trình 

Giải

Lấy (1) – (2) ta được:

Kết hợp x – y = 0 với phương trình (1) ta có hệ:  

Với x = 0 thì y = x = 0

Với x = 5 thì y = x = 5

Kết hợp x + y - 1 = 0 với phương trình (1) ta có hệ:

Với x = -1 thì y = 1 – x = 1 + 1 = 2

Với x = 2 thì y = 1 – x = 1 - 2 = -1

Vậy hệ phương trình có 4 nghiệm : (0;0), (5;5), (-1;2), (2;-1)

B. Bài tập

Câu 1: Số nghiệm của hệ phương trình 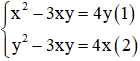 là

A. 1

B. 2

C. 3

D. 4

Giải

Lấy (1) – (2) ta được:

Kết hợp x – y = 0 với phương trình (1) ta có hệ:  

Với x = 0 thì y = x = 0

Với x = -2 thì y = x = -2

Kết hợp x + y + 4 = 0 với phương trình (1) ta có hệ:

Vậy hệ phương trình có 2 nghiệm: (0;0), (-2;-2)

Đáp án là B

Câu 2: Tìm m để hệ phương trình 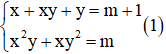 có ít nhất một nghiệm (x;y) thỏa mãn x > 0 và y > 0 là

Giải

Hệ phương trình 

Đặt 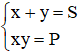. Khi đó hệ phương trình trở thành 

S, P là nghiệm của phương trình  X² – (m + 1).X + m = 0 

Suy ra S = m, P = 1 hoặc  S = 1, P = m

* Với S = m, P = 1 thì hệ (1) có nghiệm x > 0, y > 0

* Với S = 1, P = m thì hệ (1) có nghiệm x > 0, y > 0

Vậy với 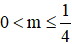 hoặc m ≥ 2 thì hệ có nghiệm thỏa mãn đầu bài

Đáp án là C

Câu 3: Tìm m để hệ phương trình 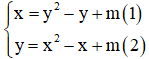 có nghiệm

Giải

Lấy (1) – (2) ta được:

Kết hợp x – y = 0 với phương trình (1) ta có hệ:

Kết hợp x + y = 0 với phương trình (1) ta có hệ:

Hệ có nghiệm khi (*) có nghiệm hoặc (**) có nghiệm

Đáp án là B

Câu 4: Số nghiệm của hệ phương trình 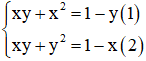 là

A. 1

B. 2

C. 3

D. vô số

Giải

Lấy (1) – (2) ta được:

Kết hợp x – y = 0 với phương trình (1) ta có hệ:

Kết hợp x + y - 1 = 0 với phương trình (1) ta có hệ:

Vậy hệ phương trình có vô số nghiệm : (-1;-1), (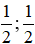) và (x;1-x) với x là số thực tùy ý

Đáp án là D

Câu 5: Trong hệ phương trình 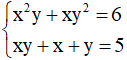 nếu đặt S = x + y và P = xy thì hệ phương trình trở thành hệ nào sau đây

Giải

Hệ phương trình 

Khi đặt S = x + y và P = xy thì hệ phương trình trở thành 

Đáp án là D

Câu 6: Số nghiệm của hệ phương trình 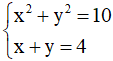 là

A. 1

B. 2

C. 3

D. 4

Giải

Với 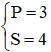  thì x, y là nghiệm của phương trình: 

Vậy hệ có hai nghiệm: (1;3), (3;1)

Đáp án là B

Câu 7: Trong hệ phương trình 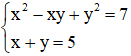 nếu đặt S = x + y và P = xy thì giá trị của S và P là

A. S = 5, P = 6

B. S = -5, P = 6

C.  S = 5, P = -6

D. S = -5, P = -6

Giải

Hệ phương trình 

Đặt S = x + y và P = xy thì hệ trở thành 

Đáp án là A

Câu 8: Tìm m để hệ phương trình 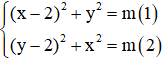 có nghiệm duy nhất

A. m = 0

B. m = 2

C. m = -3

D. m = -2

Giải

Điều kiện cần: Nếu hệ phương trình có nghiệm (x₀;y₀) thì (y₀;x₀) cũng là nghiệm của hệ

Suy ra hệ phương trình có nghiệm thì x₀ = y₀

Vì x₀ là duy nhất nên (*) có nghiệm kép ⇔ ∆ꞌ = 0

⇔ 4 – 2(4 – m) = 0

⇔ 4 – 8 + 2m = 0

⇔ 2m = 4 ⇔ m = 2

Điều kiện đủ: Với m = 2 thì hệ có dạng 

Vậy với m = 2 thì hệ có nghiệm duy nhất

Đáp án là B