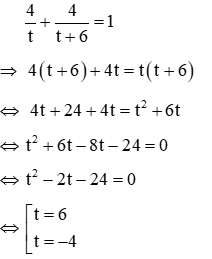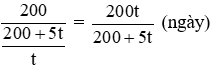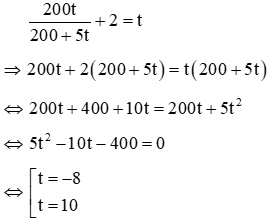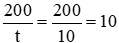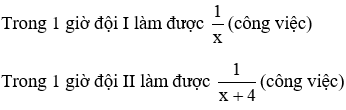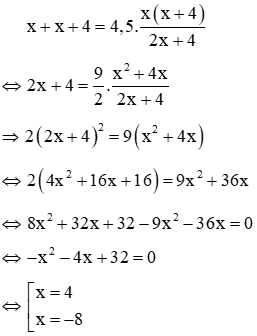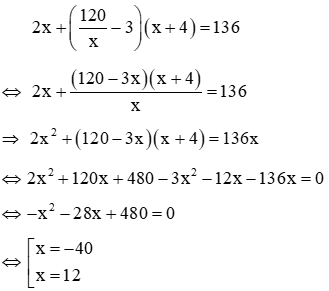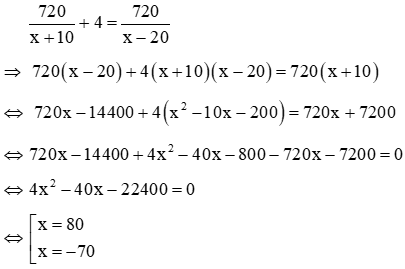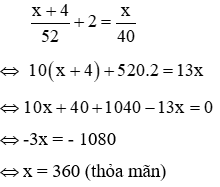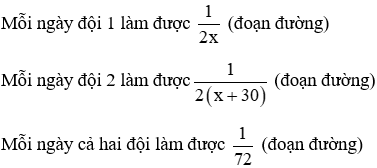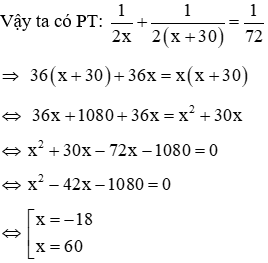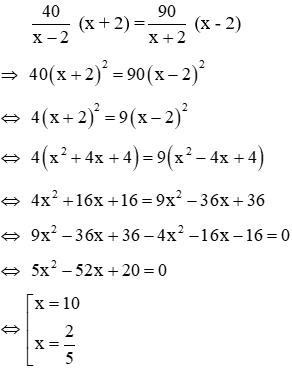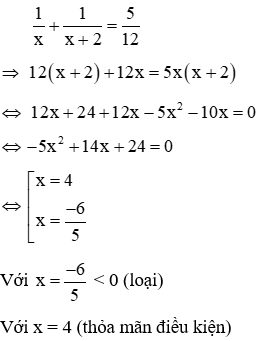Giải bài toán bằng cách lập phương trình – Dạng toán công việc

A. Phương pháp giải

B1: Lập phương trình

- Chọn ẩn số và đặt điều kiện cho ẩn

- Biểu diễn các dữ kiện chưa biết qua ẩn số

- Lập phương trình biểu thị tương quan giữa ẩn số và các dữ kiện đã biết

B2: Giải phương trình

B3: Đối chiếu nghiệm tìm được với điều kiện của ẩn số nếu có và đưa ra kết luận

Khối lượng công việc = Năng suất × Thời gian

Ví dụ 1: Hai đội công nhân cùng làm một công việc thì làm xong trong 4 giờ. Nếu mỗi đội làm một mình xong công việc ấy thì đội thứ nhất cần ít thời gian hơn đội thứ hai là 6 giờ. Hỏi mỗi đội làm một mình xong công việc trong bao lâu?( biết rằng mỗi giờ khối lượng công việc mà đội 1 làm được là như nhau và mỗi giờ khối lượng công việc mà đội 2 làm được là như nhau)

Giải

Gọi t là thời gian đội 1 làm xong công việc (t > 4, t đơn vị là giờ)

Suy ra thời gian đội 2 làm xong công việc là t + 6 (giờ)

Vì trong 4 giờ cả hai đội làm chung thì xong công việc nên ta có phương trình

Với t = -4 < 0 (loại)

Với t = 6 thỏa mãn điều kiện (nhận)

Vậy đội 1 làm xong công việc trong 6 giờ, đội 2 làm xong công việc trong 12 giờ

Ví dụ 2: Một hợp tác xã dự kiến thu hoạch 200ha lúa trong thời gian đã định. Song thực tế mỗi ngày thu hoạch nhanh hơn so với kế hoạch là 5ha nên đã hoàn thành công việc nhanh hơn dự kiến 2 ngày. Hỏi theo dự kiến mỗi ngày thu hoạch bao nhiêu ha ? (mỗi ngày thu hoạch được số lúa là như nhau)

Giải

Gọi t là số ngày hợp tác xã dự kiến thu hoạch xong 200ha lúa (t > 2)

 theo dự kiến một ngày hợp tác xã thu hoạch được số ha lúa là 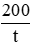 (ha)

Thực tế, mỗi ngày hợp tác thu hoạch được là: 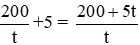 (ha)

Do đó số ngày hoàn thành công việc là:

Vì công việc hoàn thành sớm hơn dự kiến 2 ngày nên ta có phương trình:

Với t = -8 không thỏa mãn điều kiện (loại)

Với t = 10 thỏa mãn điều kiện (nhận)

Vậy theo dự kiến mỗi ngày hợp tác thu hoạch số ha lúa là 

B. Bài tập

Câu 1: Hai đội công nhân cùng làm chung một công việc. Thời gian để đội I làm một mình xong công việc ít hơn thời gian để đội II làm một mình xong công việc đó là 4 giờ. Tổng thời gian này gấp 4,5 lần thời gian hai đội cùng làm chung để xong công việc đó. Hỏi mỗi đội làm một mình thì phải bao lâu mới xong? ( biết rằng mỗi giờ khối lượng công việc mà đội 1 làm được là như nhau và mỗi giờ khối lượng công việc mà đội 2 làm được là như nhau)

A. 3 giờ và 7 giờ

B. 2 giờ và 6 giờ

C. 5 giờ và 9 giờ

D. 4 giờ và 8 giờ

Giải

Gọi thời gian đội I làm một mình xong công việc là x giờ (x > 0 )

Suy ra thời gian đội II làm một mình xong công việc là x + 4 giờ

Trong 1 giờ hai đội làm chung được: 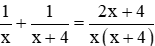 (công việc)

Thời gian để hai đội làm chung xong công việc là 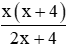 (giờ)

Vì tổng thời gian hai đội làm riêng gấp 4,5 lần thời gian hai đội làm chung để xong công việc nên ta có phương trình

Với x = -8 không thoả mãn điều kiện (loại)

Với x = 4 thoả mãn điều kiện (nhận)

Vậy Đội I làm một mình xong công việc hết 4 giờ, đội hai hết 8 giờ .

Đáp án là D

Câu 2: Một xí nghiệp giao cho một công nhân làm 120 sản phẩm trong thời gian quy định. Sau khi làm được 2 giờ, người đó cải tiến kĩ thuật nên đã tăng được 4 sản phẩm mỗi giờ so với dự kiến. Vì vậy trong thời gian quy định không những hoàn thành kế hoạch trước 1 giờ mà còn vượt mức 16 sản phẩm. Tính năng suất làm lúc đầu( biết rằng mỗi giờ xí nghiệp làm được số sản phẩm là như nhau)

A. 10 sản phẩm

B. 11 sản phẩm

C. 12 sản phẩm

D. 13 sản phẩm

Giải

Gọi số sản phẩm mà người công nhân dự kiến làm trong 1 giờ là x sản phẩm, x > 0

⇒ thời gian dự kiến làm xong 120 sản phẩm là 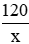 (giờ)

Sau 2 giờ đầu người đó làm được 2x (sản phẩm)

Thời gian còn lại để người đó làm là: 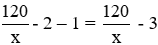 (giờ)

Sau khi cải tiến kỹ thuật mỗi giờ người đó làm được x + 4 (sản phẩm)

Vậy số sản phẩm mà người công nhân làm trong thời gian còn lại là 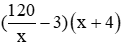 (sản phẩm)

Theo đề bài tổng số sản phẩm mà người công nhân đó làm được là 136 nên ta có phương trình

Với x = -40 < 0 (loại)

Với x = 12 > 0 (nhận)

Vậy năng suất dự kiến lúc đầu là 12 sản phẩm trong 1 giờ

Đáp án là C

Câu 3: Một tổ dự định sản xuất 720 sản phẩm theo năng suất dự định. Nếu sản xuất tăng 10 sản phẩm mỗi ngày sẽ nhanh hơn giảm năng suất 20 sản phẩm mỗi ngày là 4 ngày. Tính năng suất dự kiến ban đầu ( biết rằng mỗi ngày tổ làm được số sản phẩm là như nhau)

A. 50 sản phẩm

B. 60 sản phẩm

C. 70 sản phẩm

D. 80 sản phẩm

Giải

Gọi x là số sản phẩm dự kiến ban đầu làm trong 1 ngày, x > 20

Nếu sản xuất tăng 10 sản phẩm mỗi ngày thì số ngày làm xong 720 sản phẩm là 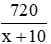 (ngày)

Nếu sản xuất giảm 20 sản phẩm mỗi ngày thì số ngày làm xong 720 sản phẩm là 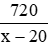 (ngày)

Vì nếu sản xuất tăng 10 sản phẩm mỗi ngày sẽ nhanh hơn giảm năng suất 20 sản phẩm mỗi ngày là 4 ngày nên ta có phương trình

Với x = -70 < 0(loại)

Với x = 80 (thỏa mãn điều kiện )

Vậy số sản phẩm dự kiến ban đầu làm trong 1 ngày là 80 sản phẩm

Đáp án là D

Câu 4: Một đội máy kéo dự định mỗi ngày cày 40 ha. Khi thực hiện mỗi ngày cày được 52 ha vì vậy đội không những cày xong trước thời hạn 2 ngày mà còn cày thêm được 4 ha nữa. Tính diện tích thửa ruộng mà đội phải cày theo kế hoạch ( biết rằng mỗi ngày đội máy kéo cày được diện tích là như nhau)

A. 320 ha

B. 330 ha           

C. 340 ha

D. 360 ha

Giải

Gọi diện tích mà đội phải cày theo kế hoạch là x(ha), x > 0

Thời gian đội dự định hoàn thành công việc là 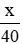 (ngày)

Diện tích thực tế mà đội cày được là x + 4 (ha)

Thời gian thực tế đội hoàn thành công việc là 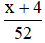 (ngày)

Vì thời gian thực tế ít hơn thời gian dự kiến 2 ngày nên ta có phương trình

Vậy số diện tích mà đội phải cày theo kế hoạch là 360 (ha)

Đáp án là D

Câu 5: Hai đội công nhân làm một đoạn đường. Đội 1 làm xong một nửa đoạn đường thì đội 2 đến làm tiếp nửa còn lại với thời gian dài hơn thời gian đội 1 đã làm là 30 ngày. Nếu hai đội cùng làm thì trong 72 ngày xong cả đoạn đường .Hỏi mỗi đội đã làm bao nhiêu ngày trên đoạn đường này? (biết rằng mỗi ngày khối lượng công việc mà đội 1 làm được là như nhau và mỗi ngày khối lượng công việc mà đội 2 làm được là như nhau)

A. 60 ngày và 90 ngày

B. 50 ngày và 80 ngày

C. 70 ngày và 10 ngày

D. 40 ngày và 70 ngày

Giải

Gọi thời gian đội 1 làm xong nửa đoạn đường là x ngày (x > 0)

⇒ thời gian đội 2 làm xong nửa đoạn đường còn lại là x + 30 ( ngày )

Với x = -18 không thoả mãn điều kiện (loại)

Với x = 60 thoả mãn điều kiện (nhận)

Vậy đội 1 làm trong 60 ngày , đội 2 làm trong 90 ngày .

Đáp án là A

Câu 6: Hai đội công nhân trồng rừng phải hoàn thành kế hoạch trong cùng một thời gian. Đội 1 phải trồng 40 ha, đội 2 phải trồng 90 ha. Đội 1 hoàn thành công việc sớm hơn 2 ngày so với kế hoạch. Đội 2 hoàn thành muộn hơn 2 ngày so với kế hoạch. Nếu đội 1 làm công việc trong một thời gian bằng thời gian đội 2 đã làm và đội 2 làm trong thời gian bằng đội 1 đã làm thì diện tích trồng được của hai đội bằng nhau. Tính thời gian mỗi đội phải làm theo kế hoạch? (biết rằng mỗi ngày diện tích rừng mà đội 1 trồng được là như nhau và mỗi ngày diện tích rừng mà đội 2 trồng được là như nhau)

A. 12 ngày

B. 8 ngày

C. 10 ngày

D. 9 ngày

Giải

Gọi thời gian mỗi đội phải làm theo kế hoạch là x (ngày), (x > 2, x ∈ N)

Thời gian đội 1 đã làm là x – 2 ( ngày )

Thời gian đội 2 đã làm là x + 2 ( ngày )

Nếu đội 1 làm trong x + 2 ngày thì trồng được 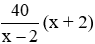 (ha)

Nếu đội 2 làm trong x - 2 ngày thì trồng được 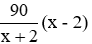 (ha)

Theo đầu bài diện tích rừng trồng được của hai đội trong trường này là bằng nhau nên ta có phương trình:

Với x = 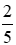 không thoả mãn điều kiện (loại)

Với x = 10 thoả mãn điều kiện (nhận)

Vậy theo kế hoạch mỗi đội phải làm việc 10 ngày.

Đáp án là C

Câu 7: Hai người cùng làm chung một công việc trong 12/5 giờ thì xong. Nếu mỗi người làm một mình thì người thứ nhất hoàn thành xong công việc ít hơn người thứ hai là 2 giờ. Hỏi nếu mỗi người làm một mình thì làm trong bao lâu để xong công việc( biết rằng mỗi giờ người thứ nhất làm được khối lượng công việc là như nhau và mỗi giờ người thứ hai làm được khối lượng công việc là như nhau)

A. 3 giờ và 7 giờ

B. 4 giờ và 6 giờ

C. 4 giờ và 8 giờ

D. 5 giờ và 6 giờ

Giải

Gọi thời gian người thứ nhất làm một mình xong công việc là x (giờ), x > 0

Thời gian người thứ hai làm một mình xong công việc là x + 2 (giờ)

Trong 1 giờ cả hai người làm được 5/12 công việc nên ta có phương trình

Vậy người thứ nhất làm một mình xong công việc trong 4 giờ, người thứ hai làm một mình xong công việc trong 6 giờ

Đáp án là B