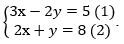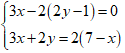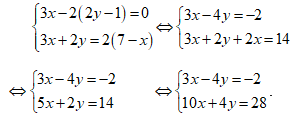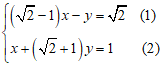Cách giải hệ phương trình bằng phương pháp cộng đại số cực hay
Với Cách giải hệ phương trình bằng phương pháp cộng đại số cực hay Toán học lớp 9 với đầy đủ lý thuyết, phương pháp giải và bài tập có lời giải cho tiết sẽ giúp học sinh nắm được Cách giải hệ phương trình bằng phương pháp cộng đại số cực hay.
Cách giải hệ phương trình bằng phương pháp cộng đại số cực hay
A. Phương pháp giải
Bước 1: Nhân hai vế của mỗi phương trình với một số thích hợp(nếu cần) sao cho các hệ số của một ẩn nào đó(ẩn x hay y) trong hai phương trình của hệ bằng nhau hoặc đối nhau.
Bước 2: Cộng hay trừ từng vế hai phương trình của hệ phương trình đã cho để được một phương trình mới
Bước 3: Dùng phương trình mới ấy thay thế cho một trong hai phương trình của hệ (và giữ nguyên phương trình kia)
Bước 4: Giải phương trình một ẩn vừa thu được rồi suy ra nghiệm của hệ đã cho.
Bước 5: Kết luận
B. Ví dụ minh họa
Ví dụ 1: Giải hệ phương trình sau: 
Hướng dẫn:
Nhân hai vế của pt (2) với 2 ta được:
Cộng các vế tương ứng của hai phương trình ta có: 7x = 21 ⇔ x = 3.
Thay vào phương trình (2) ta được: 6 + y = 8 ⇔ y = 2
Vậy nghiệm của hệ phương trình là (x;y) = (3;2).
Ví dụ 2: Giải hệ phương trình sau: 
Hướng dẫn:
Ta có:
Cộng các vế tương ứng của hai phương trình ta có: 13x = 26 ⇔ x = 2.
Thay x = 2 vào phương trình thứ hai: 5.2 + 2y = 14 ⇔ y = 2.
Vậy nghiệm của hệ phương trình là (x;y) = (2;2).
Ví dụ 3: Giải hệ phương trình: 
Hướng dẫn:
Bài viết liên quan
- Vẽ thêm yếu tố phụ để giải một số bài toán về đường tròn
- Phương pháp giải hệ phương trình bậc nhất hai ẩn siêu hay, chi tiết
- Cách giải hệ phương trình bậc nhất hai ẩn cực hay, có lời giải
- Cách giải hệ phương trình bằng phương pháp đặt ẩn phụ cực hay
- Cách giải hệ phương trình bậc nhất hai ẩn chứa tham số cực hay
