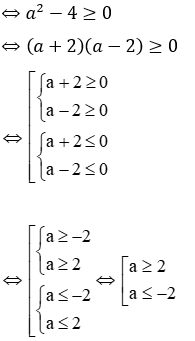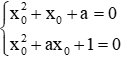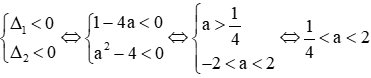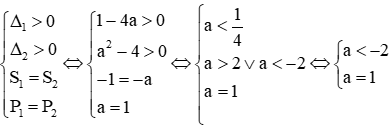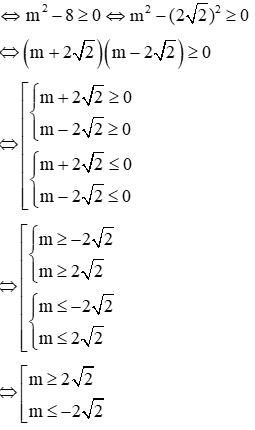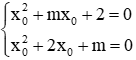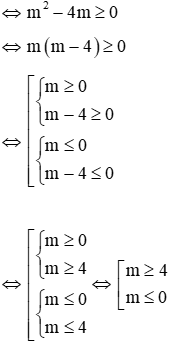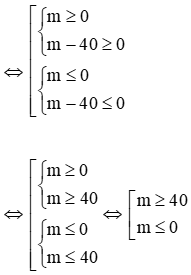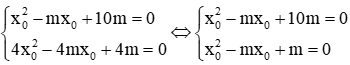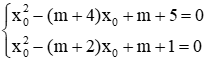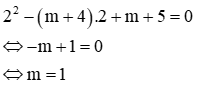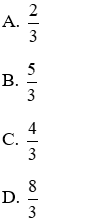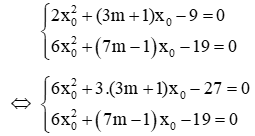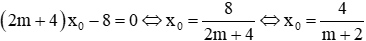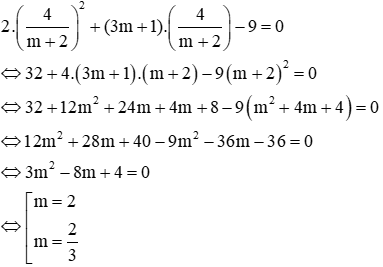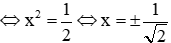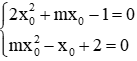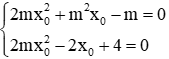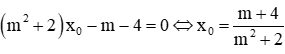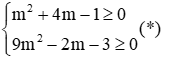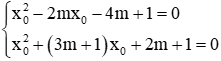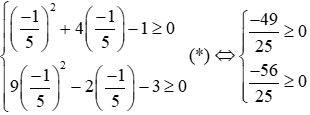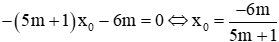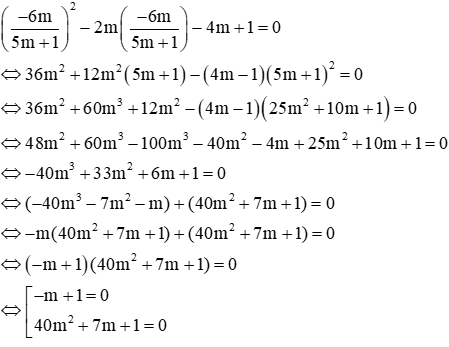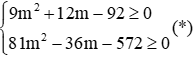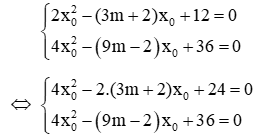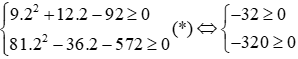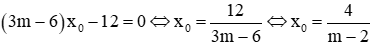Cách tìm m để hai phương trình có nghiệm chung cực hay

A. Phương pháp giải

- Bài toán: Cho 2 phương trình dạng ax² + bx + c = 0 có chứa tham số m. Tìm m để 2 phương trình có ít nhất một nghiệm chung

- Cách giải:

+ B1: Tìm điều kiện của m để 2 phương trình cùng có nghiệm

+ B2: Giả sử x₀ là nghiệm chung của 2 phương trình. Tìm x₀

+ B3: Thế x₀ tìm được vào một trong hai phương trình tìm m

+ B4: Đối chiếu m tìm được với điều kiện ở B₁, nếu thỏa mãn thì nhận, không thỏa mãn thì loại

Ví dụ 1: Cho 2 phương trình : x² + x + a = 0(1) và x² + ax + 1 = 0(2).

a. Tìm a để 2 phương trình  có ít nhất một nghiệm chung

b. Tìm a để 2 phương trình tương đương

Giải

a. Phương trình (1) có nghiệm khi: Δ ≥ 0 ⇔ 1 – 4a ≥ 0 ⇔ a ≤ 1/4

Phương trình (2 ) có nghiệm khi: Δ ≥ 0

Điều kiện để 2 phương trình cùng có nghiệm là: a ≤ -2  (*)

Giả sử x₀ là nghiệm chung của 2 phương trình (2) ta có: 

Trừ 2 phương trình cho nhau ta được: x₀(1 – a) – (1 – a) = 0

⇔   x₀(1 – a) = (1 – a) (**)

Vì a ≤ -2  nên 1 – a luôn khác 0. Chia hai vế của (**) cho 1 – a ta được x₀ = 1

Thay x₀ = 1 vào (1) ta có: a = -2 ( thỏa mãn (*))

Vậy với a = -2 thì 2 phương trình  có ít nhất một nghiệm chung

b. Kí hiệu ∆₁, S₁, P₁ lần lượt là biệt thức đen-ta, tổng 2 nghiệm, tích 2 nghiệm của phương trình (1)

Kí hiệu ∆₂, S₂, P₂ lần lượt là biệt thức đen-ta, tổng 2 nghiệm, tích 2 nghiệm l của phương trình (2)

Hai phương trình tương đương khi chúng có cùng tập nghiệm . Ta xét các trường hợp sau:

+ TH₁: Hai phương trình cùng có tập nghiệm là rỗng

Trường hợp này xảy ra khi: 

+ TH₂: Hai phương trình có nghiệm kép giống nhau

Trường hợp này xảy ra khi 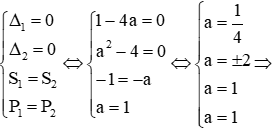 vô nghiệm

+ TH₃: Hai phương trình có nghiệm phân biệt giống nhau

Trường hợp này xảy ra khi 

⇒ vô nghiệm

Vậy với 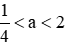 thì 2 phương trình đã cho tương đương

Ví dụ 2: Cho 2 phương trình : x² + mx + 2 = 0(1) và x² + 2x + m = 0(2). Tìm m để hai phương trình có ít nhất một nghiệm chung

Giải

Phương trình (1) có nghiệm khi: Δ ≥ 0

Phương trình (2 ) có nghiệm khi: Δ' ≥ 0 ⇔ 1 - m ≥ 0 ⇔ m ≤ 1

⇒ Điều kiện để 2 phương trình cùng có nghiệm là m ≤ -2√2 (*)

Giả sử x₀ là nghiệm chung của 2 phương trình, ta có: 

Trừ 2 phương trình cho nhau ta được: mx₀ - 2x₀ + 2 - m = 0 ⇔ (m - 2)x₀ = m - 2

Do m ≤ -2√2 nên m – 2 ≠ 0, suy ra x₀ = 1

Thay x₀ = 1 vào phương trình (1): 1 + m + 2 = 0 hay m = -3( thỏa mãn (*))

Vậy với m = -3 thì 2 phương trình có ít nhất một nghiệm chung

Ví dụ 3: Cho 2 phương trình : x² - 2mx + 4m = 0(1) và x² - mx + 10m = 0(2) . Tìm m để phương trình (2) có một nghiệm gấp 2 lần một nghiệm của phương trình (1)

Giải

Phương trình (1) có nghiệm khi: Δ' ≥ 0

Phương trình (2 ) có nghiệm khi: Δ ≥ 0

⇔ m² - 40m ≥ 0 ⇔ m(m - 40) ≥ 0

⇒ Điều kiện để 2 phương trình cùng có nghiệm là m ≥ 40 ∨ m ≤ 0 (*)

Giả sử x₀ là nghiệm của phương trình (2) thì 2x₀ là nghiệm của phương trình (1). Thay x₀ vào (2) và 2x₀ vào (1) ta có:     

Trừ 2 phương trình cho nhau ta được: 9m = 0 ⇔ m = 0 (thỏa mãn (*))

Vậy với m = 0 thì phương trình (2) có một nghiệm gấp 2 lần một nghiệm của phương trình (1)

B. Bài tập

Câu 1: Cho hai phương trình x² – (m + 4)x + m + 5 = 0 (1) và x² – (m + 2)x + m + 1 = 0 (2), khẳng định nào sau đây là đúng

A. Có một giá trị của m để hai phương trình có nghiệm chung

B. Tích các giá trị của m để hai phương trình có nghiệm chung bằng 10

C. Giá trị của m để hai phương trình có nghiệm chung là số lớn hơn 3

D. Không có giá trị của m để hai phương trình có nghiệm chung

Giải

Phương trình (1) có nghiệm khi: Δ ≥ 0 ⇔ (m + 4)² - 4(m + 5) ≥ 0

⇔ m² + 8m + 16 - 4m - 20 ≥ 0 ⇔ m² + 4m - 4 ≥ 0

Phương trình (2 ) có nghiệm khi: Δ ≥ 0 ⇔ (m + 2)² - 4(m + 1) ≥ 0

⇔ m² + 4m + 4-4m - 4 ≥ 0 ⇔ m² ≥ 0,(∀ m ∈ R)

⇒ Điều kiện để hai phương trình luôn có nghiệm là: m² + 4m – 4 ≥  0(*)

Giả sử x₀ là nghiệm chung của 2 phương trình, ta có:

Trừ 2 phương trình cho nhau ta được:  -(m + 4)x₀ + (m + 2)x₀ + 4 = 0 ⇔ -2x₀ + 4 = 0 ⇔ x₀ = 2

Thay  vào phương trình (1):

Với m = 1 thì m² + 4m – 4 = 1 + 4 – 4 = 1 > 0 thỏa mãn điều kiện (*)nên nhận

Vậy với m = 1 thì 2 phương trình có nghiệm chung

Đáp án A

Câu 2: Tổng các giá trị của m để hai phương trình 2x² + (3m + 1)x - 9 = 0 (1) và 6x² + (7m - 1)x - 19 = 0 (2) có nghiệm chung là

Giải

Phương trình (1) có nghiệm khi: Δ ≥ 0 ⇔ (3m + 1)² - 4.2.(-9) ≥ 0 ⇔ (3m + 1)² + 72 ≥ 0,(∀ m ∈ R)

Phương trình (2) có nghiệm khi: Δ ≥ 0 ⇔ (7m - 1)² - 4.6.(-19) ≥ 0 ⇔ (7m-1)² + 456 ≥ 0,(∀ m ∈ R)

⇒ Với mọi m hai phương trình luôn có nghiệm

Giả sử x₀ là nghiệm chung của 2 phương trình, ta có:

Trừ 2 phương trình cho nhau ta được: (9m + 3)x₀-(7m-1)x₀-27+19=0 ⇔ (2m + 4)x₀-8=0(*)

Nếu m = -2 thì phương trình  (*)  vô nghiệm

Nghĩa là với m = -2 thì 2 phương trình cùng không có nghiệm chung

Vậy muốn hai phương trình có nghiệm chung thì m ≠ -2

Khi m ≠ -2 thì 

Thay  vào phương trình (1):

Vậy với m = 2, 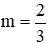 thì 2 phương trình có nghiệm chung

Đáp án D

Câu 3: Tích các giá trị của m để hai phương trình 2x² + mx - 1 = 0 (1) và mx² - x + 2 = 0 (2) có nghiệm chung là

A. -1

B. 5

C. 8

D. -10

Giải

+) TH1: m = 0 thì phương trình (1): 2x² - 1 = 0 

Phương trình (2): -x + 2 = 0 ⇔  x = 2

⇒ với m = 0 thì hai phương trình không có nghiệm chung

+) TH2: m ≠ 0 thì hai phương trình đều là phương trình bậc hai. Khi đó

Phương trình (1) có nghiệm khi Δ ≥ 0 m² + 8 ≥ 0,(∀ m ∈ R)

Phương trình (2 ) có nghiệm khi Δ ≥ 0 ⇔ 1 - 8m ≥ 0 ⇔ m ≤ 1/8

⇒ Với 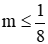 hai phương trình luôn có nghiệm

Giả sử x₀ là nghiệm chung của 2 phương trình, ta có: 

Vì m ≠ 0 nên ta nhân 2 vế của phương trình thứ nhất với m, nhân 2 vế của phương trình thứ hai với 2 ta được:

Trừ 2 phương trình cho nhau ta được:

Thay vào phương trình (1):

Xét phương trình m² – m + 7 = 0 có ∆ = (-1)² – 4.1.7 = -27 < 0 nên vô nghiệm

Vậy với m = -1 thì 2 phương trình có nghiệm chung

Đáp án A

Câu 4: Số giá trị của m để hai phương trình x² – 2mx – 4m + 1 = 0 (1) và x² + (3m + 1)x + 2m + 1 = 0 (2) có nghiệm chung là

A. 0

B. 1

C. 2

D. 3

Giải

Phương trình (1) có nghiệm khi  Δ' ≥ 0 ⇔ m² + 4m - 1 ≥ 0

Phương trình (2 ) có nghiệm khi Δ ≥ 0 ⇔ (3m + 1)² - 4(2m + 1) ≥ 0 ⇔ 9m² - 2m - 3 ≥ 0

Điều kiện để hai phương trình có nghiệm là:

Giả sử x₀ là nghiệm chung của 2 phương trình, ta có: 

Trừ 2 phương trình cho nhau ta được: -2mx₀ - (3m + 1)x₀ - 4m + 1 - 2m - 1 = 0 ⇔ -(5m + 1)x₀ - 6m = 0

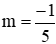
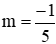
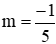
Nếu   thì 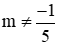điều kiện (*) trở thành 

⇒   không thỏa mãn (*), nghĩa là với  thì hai phương trình đều vô nghiệm. Vậy muốn hai phương trình có nghiệm chung thì 

Khi  thì 

Thay  vào phương trình (1):

Xét –m + 1 = 0 ⇔  m = 1( thỏa mãn (*)) ⇒ nhận

Xét 40m² + 7m + 1 = 0 có ∆ = 7² -4.40.1 = -111 < 0 nên vô nghiệm

Vậy với m = 1 thì 2 phương trình có nghiệm chung

Đáp án B

Câu 5: Số giá trị của m để hai phương trình 2x² – (3m + 2)x + 12 = 0 (1) và 4x² - (9m - 2)x + 36 = 0 (2) có nghiệm chung là

A. 0

B. 1

C. 2

D. 3

Giải

Phương trình (1) có nghiệm khi: Δ ≥ 0 ⇔ (3m + 2)² - 4.2.12 ≥ 0 ⇔ 9m² + 12m - 92 ≥ 0

Phương trình (2) có nghiệm khi: Δ ≥ 0 ⇔ (9m - 2)² - 4.4.36 ≥ 0 ⇔ 81m² - 36m + 4 - 576 ≥ 0 ⇔ 81m² - 36m - 572 ≥ 0

Điều kiện để hai phương trình có nghiệm là: 

Giả sử x₀ là nghiệm chung của 2 phương trình, ta có:

Trừ 2 phương trình cho nhau ta được: -(6m + 4)x₀ + (9m - 2)x₀ - 12 = 0 ⇔ (3m - 6)x₀ - 12 = 0

Nếu m = 2 thì điều kiện (*) trở thành: 

⇒ m = 2 không thỏa mãn (*), nghĩa là với m = 2 thì 2 phương trình cùng vô nghiệm

Vậy muốn hai phương trình có nghiệm chung thì m ≠ 2

Khi m ≠ 2 thì 

Thay vào phương trình (1):

Xét m = 3( thỏa mãn (*)) ⇒ nhận

Vậy với m = 3 thì 2 phương trình có nghiệm chung

Đáp án B