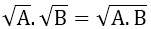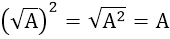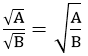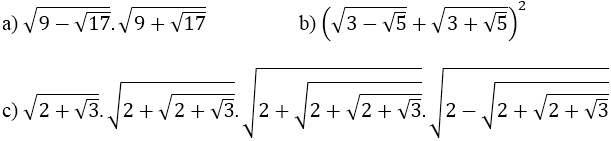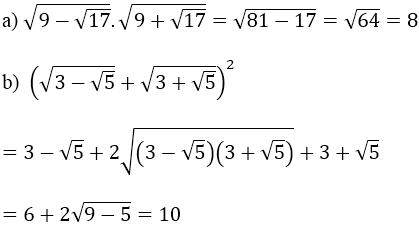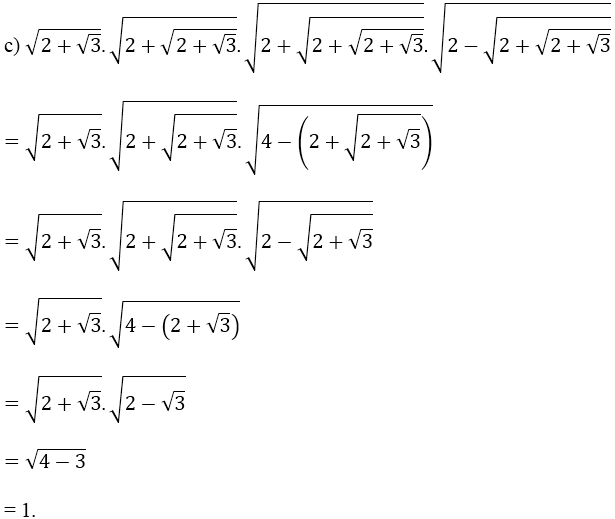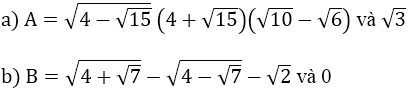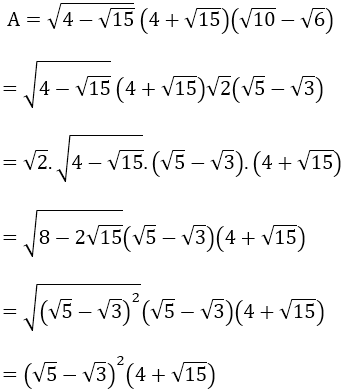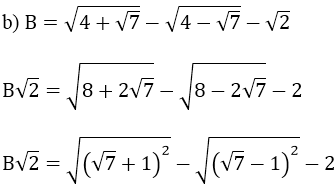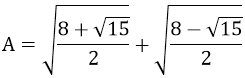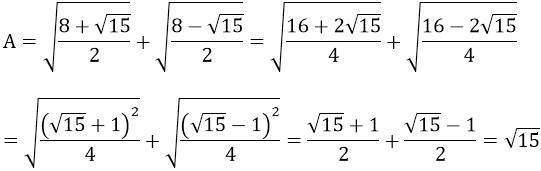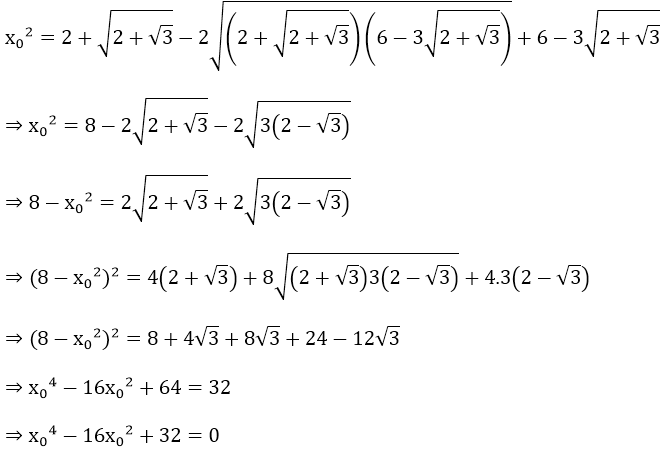Liên hệ giữa phép nhân, phép chia với phép khai phương
Với Liên hệ giữa phép nhân, phép chia với phép khai phương Toán học lớp 9 với đầy đủ lý thuyết, phương pháp giải và bài tập có lời giải cho tiết sẽ giúp học sinh nắm được Liên hệ giữa phép nhân, phép chia với phép khai phương.
Liên hệ giữa phép nhân, phép chia với phép khai phương
Lý thuyết và Phương pháp giải
1. Với A ≥ 0, B ≥ 0 thì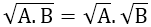 
và ngược lại 
Đặc biệt, khi A ≥ 0, ta có: 
2. Với A ≥ 0,B >0 thì: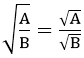 
và ngược lại 
3. Bổ sung
+) Với A1 , A2, ... , An ≥ 0 thì 
+) Với a ≥ 0; b ≥ 0 thì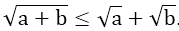 
. Dấu bằng xảy ra khi a = 0 hoặc b = 0
+) Với a ≥ b ≥ 0 thì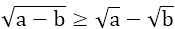 
. Dấu bằng xảy ra khi a = 0 hoặc b = 0
4. Các bất đẳng thức thường dùng
+) Với a ≥ b ≥ 0 thì 
+) 
với a > 0; b > 0
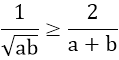
Ví dụ minh họa
Ví dụ 1: Thực hiện phép tính:
Hướng dẫn:
Ví dụ 2: Cho các biểu thức 
a) Tìm các giá trị của x để M và N có nghĩa.
b) Với giá trị nào của x thì M = N.
Hướng dẫn:
a) M có nghĩa khi (x - 1)(x + 3) ≥ 0
Trường hợp 1: 
Trường hợp 2: 
Vậy M có nghĩa khi x ≥ 1 hoặc x ≤ -3
N có nghĩa khi 
b) Để M và N đồng thời có nghĩa thì x ≥ 1
Khi đó ta có M = N theo quy tắc khai phương một tích.
Ví dụ 3: So sánh:
Hướng dẫn:
a) Ta có:
= (8 - 2√15)(4 + √15)
= 2(4 - √15)(4 + √15)
= 2(16 - 15) = 2
Vậy A = 2 = √4 > √3.
B√2 = √7 + 1 - (√7 - 1) - 2
B√2 = 0
⇒ B = 0
Ví dụ 4: Rút gọn biểu thức:
Hướng dẫn:
Vậy A = √15
Ví dụ 5: Chứng minh rằng số 
là một nghiệm của phương trình x4 - 16x2 + 32 = 0
Hướng dẫn:
Ta có:
Vậy xo là một nghiệm của phương trình x4 - 16x2 + 32=0
