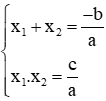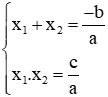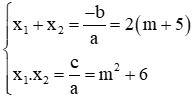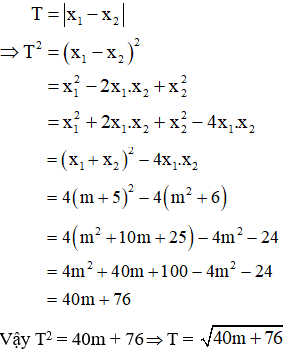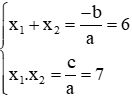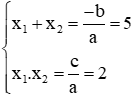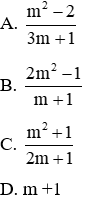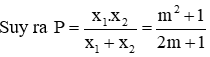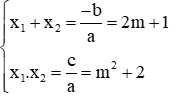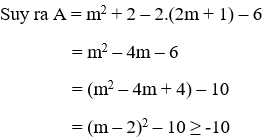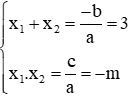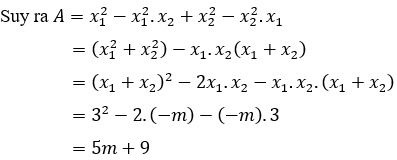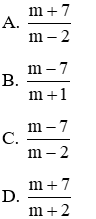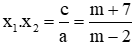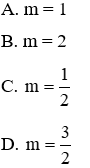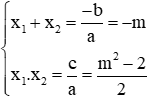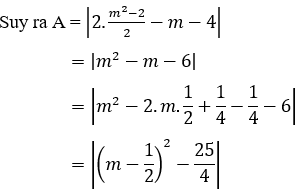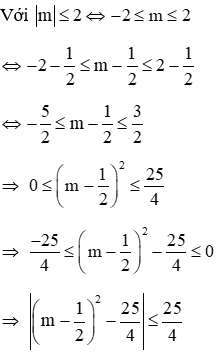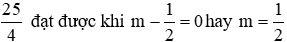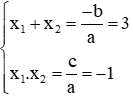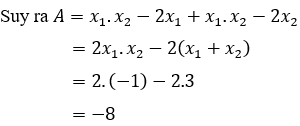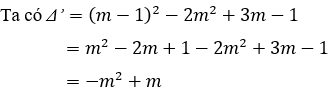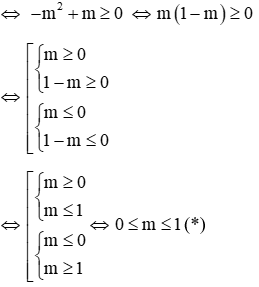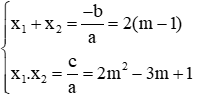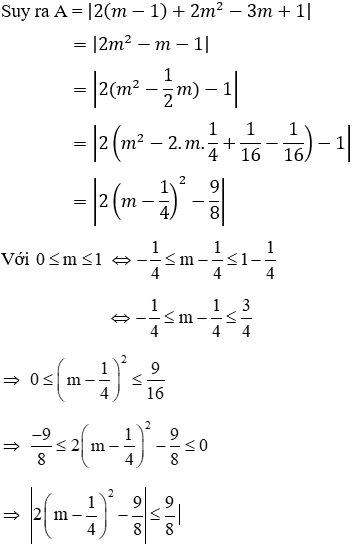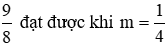Không giải phương trình, tính tổng và tích các nghiệm của phương trình bậc hai

A. Phương pháp giải

- Định lý Vi-et: Nếu x₁, x₂ là hai nghiệm của phương trình ax² + bx + c = 0 (a ≠ 0) thì

- Sử dụng định lý Vi-et không cần giải phương trình ta vẫn có thể tính được tổng và tích các nghiệm hoặc các biểu thức có liên quan đến tổng và tích các nghiệm thông qua các bước sau:

+ B1: Tính ∆ = b² – 4ac. Nếu ∆ < 0 thì phương trình vô nghiệm do đó  không tồn tại tổng và tích các nghiệm của phương trình. Nếu  ∆ ≥ 0 thì phương trình có 2 nghiệm x₁, x₂, ta thực hiện bước 2

+ B2: Trong trường hợp ∆ ≥ 0 áp dụng Vi-et ta có: 

Ví dụ 1: Biết x₁, x₂ là 2 nghiệm của phương trình: x² – 2(m + 5)x + m² + 6 = 0.

Không giải phương trình tính

a. Tổng và tích các nghiệm theo m

b. Tính giá trị của biểu thức T = |x₁ - x₂| theo m

Giải

a. Vì phương trình có 2 nghiệm x₁, x₂ nên theo Vi-et ta có:    

b. Ta có:

Ví dụ 2: Không giải phương trình, tính tổng và tích các nghiệm (nếu có) của các phương trình sau

a. x² – 6x + 7 = 0

b. 5x² – 3x + 1 = 0

Giải

a. Ta có ∆ꞌ = (bꞌ)² – ac = (-3)² – 7 = 9 – 7 = 2 > 0 nên phương trình có 2 nghiệm phân biệt x₁, x₂

Theo Vi-et ta có: 

Vậy tổng 2 nghiệm bằng 6, tích 2 nghiệm bằng 7

b. Ta có ∆ = b² – 4ac = (-3)² – 4.5.1 = 9 – 20 = -11 < 0 nên phương trình vô nghiệm

Suy ra không tồn tại tổng và tích các nghiệm

Ví dụ 3: Biết x₁, x₂ là 2 nghiệm của phương trình: x² – 5x + 2 = 0. Không giải phương trình tính giá trị của biểu thức A = x₁² + x₂²

Giải

Vì phương trình có 2 nghiệm x₁, x₂ nên theo Vi-et ta có: 

A = x₁² + x₂² = (x₁ + x₂)²-2x₁.x₂ = 5² - 2.2 = 25 - 4 = 21

Vậy A = 21

B. Bài tập

Câu 1: Biết x₁, x₂ là 2 nghiệm của phương trình  x² – (2m + 1)x + m² +1 = 0. Tính giá trị của biểu thức 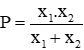 theo m

Giải

Vì phương trình có 2 nghiệm x₁, x₂ nên theo Vi-et ta có: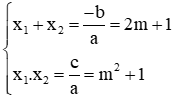  

Đáp án đúng là C.

Câu 2: Gọi x₁, x₂ là 2 nghiệm của phương trình  x² – (2m + 1)x + m² +2 = 0. Tìm m để biểu thức A = x₁.x₂ – 2(x₁ + x₂) – 6 đạt giá trị nhỏ nhất

A. m = 1              

B. m = 2               

C. m = -12           

D. m = 3

Giải

Giả sử phương trình có 2 nghiệm x₁, x₂ theo Vi-et ta có: 

Vậy giá trị nhỏ nhất của A là -10 đạt được khi m – 2 = 0 hay m = 2

Thay m = 2 vào phương trình ta được: x² – 5x + 6 = 0.

Phương trình có 2 nghiệm phân biệt x₁ = 2, x₂ = 3.

Suy ra m = 2 (thỏa mãn)

Đáp án đúng là B 

Câu 3: Biết x₁, x₂ là 2 nghiệm của phương trình  x² - 3x - m = 0.

Tính giá trị của biểu thức A = x₁²(1 - x₂) + x₂²(1-x₁)

A. –m + 9            

B. 5m + 9             

C. m + 9              

D. -5m + 9

Giải

Vì phương trình có 2 nghiệm x₁, x₂ nên theo Vi-et ta có: 

Vậy đáp án đúng là B

Câu 4: Biết x₁, x₂ là 2 nghiệm của phương trình  (m - 2)x² – (2m + 5)x + m +7 = 0 (m ≠ 2). Tính tích các nghiệm theo m

Giải

Vì phương trình có 2 nghiệm x₁, x₂ nên theo Vi-et ta có: 

Đáp án đúng là A

Câu 5: Gọi x₁, x₂ là 2 nghiệm của phương trình  2x² + 2mx + m² - 2 = 0. Tìm m để  biểu thức A = |2x₁x₂ + x₁ + x₂ - 4| đạt giá trị lớn nhất

Giải

Ta có: Δ' = m² - 2m² + 4 = -m² + 4  

Phương trình có hai nghiệm khi Δ' ≥ 0 ⇔ -m² + 4 ≥ 0 ⇔ m² ≤ 4 ⇔ |m| ≤ 2 (*)

Giả sử phương trình có 2 nghiệm x₁, x₂ theo Vi-et ta có:  

Vậy giá trị lớn nhất của A là 

Ta thấy 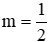 (thỏa mãn (*))

Đáp án đúng là C 

Câu 6: Tổng 2 nghiệm của phương trình  2x² – 10x + 3 = 0 là

A. 5  

B. -5           

C. 0                 

D. Không tồn tại

Giải

Ta có ∆ꞌ = (bꞌ)² – ac = (-5)² – 3.2 = 25 – 6 = 19 > 0 nên phương trình có 2 nghiệm phân biệt x₁, x₂

Theo Viet ta có: x₁ + x₂ = 5.

Vậy đáp án đúng là A

Câu 7: Tích 2 nghiệm của phương trình  x² – x + 2 = 0 là

A. -2          

B. 2              

C. 1            

D. Không tồn tại

Giải

Ta có ∆ = b² – 4ac = (-1)² – 4.1.2 = 1 – 8 = -7 < 0 nên phương trình vô nghiệm.

 Suy ra không tồn tại tích 2 nghiệm

Vậy đáp án đúng là D

Câu 8: Biết x₁, x₂ là 2 nghiệm của phương trình - x² + 3x + 1 = 0.

 Khi đó giá trị của biểu thức là A = x₁(x₂ - 2) + x₂(x₁ - 2)

A. -7          

B. -8             

C. -6          

D. Không tồn tại

Giải

Vì phương trình có 2 nghiệm x₁, x₂ nên theo Vi-et ta có:  

Vậy đáp án đúng là B

Câu 9: Gọi x₁, x₂ là 2 nghiệm của phương trình  x² - 2(m – 1)x + 2m² – 3m + 1 = 0. Tìm m để biểu thức A = |x₁x₂ + x₁ + x₂| đạt giá trị lớn nhất

Ta thấy 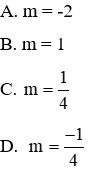 (thỏa mãn (*))

Giải

Phương trình có hai nghiệm khi Δ' ≥ 0

Giả sử phương trình có 2 nghiệm x₁, x₂ theo Vi-et ta có: 

Vậy giá trị lớn nhất của A là 

Ta thấy 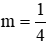 (thỏa mãn *)

Đáp án đúng là C