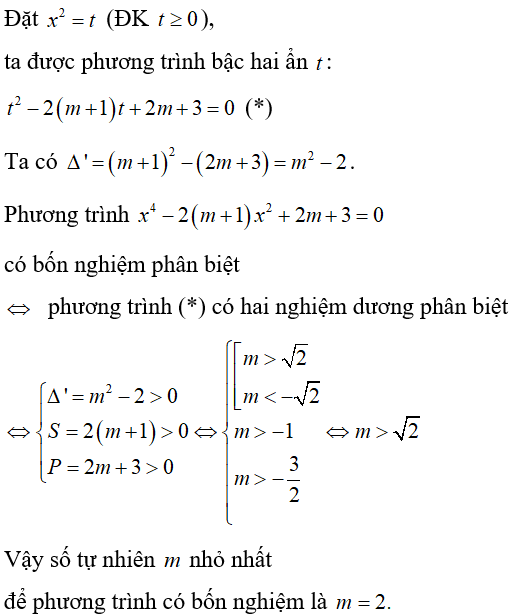Cách giải phương trình trùng phương cực hay, có đáp án
Với Cách giải phương trình trùng phương cực hay, có đáp án Toán học lớp 9 với đầy đủ lý thuyết, phương pháp giải và bài tập có lời giải cho tiết sẽ giúp học sinh nắm được Cách giải phương trình trùng phương cực hay, có đáp án
Cách giải phương trình trùng phương cực hay, có đáp án
A. Phương pháp giải
Giải phương trình trùng phương: Cho phương trình ax4 + bx2 + c = 0 (a ≠ 0) (1)
Bước 1: Đặt x2 = t (ĐK t ≥ 0), ta được phương trình bậc hai ẩn t: at2 + bt + c = 0 (a ≠ 0) (2)
Bước 2: Giải phương trình bậc hai ẩn t.
Bước 3: Giải phương trình x2 = t để tìm nghiệm .
Bước 4: Kết luận.
Biện luận số nghiệm của phương trình trùng phương
+) Phương trình (1) có 4 nghiệm phân biệt ⇒ phương trình (2) có 2 nghiệm dương phân biệt.
+) Phương trình (1) có 3 nghiệm phân biệt ⇒ phương trình (2) có 1 nghiệm dương và một nghiệm t = 0.
+) Phương trình (1) có 2 nghiệm phân biệt ⇒ phương trình (2) có 2 nghiệm trái dấu hoặc có nghiệm kép dương.
+) Phương trình (1) có duy nhất 1 nghiệm ⇒ phương trình (2) có nghiệm kép x = 0 hoặc có một nghiệm x = 0 và một nghiệm âm.
+) Phương trình (1) vô nghiệm ⇒ phương trình (2) vô nghiệm hoặc có hai nghiệm âm.
B. Các ví dụ điển hình
Ví dụ 1: Số nghiệm của phương trình x4 - 6x2 + 8 = 0 là:
Lời giải
Chọn D
Ví dụ 2: Phương trình x4 + 2(m + 1)x2 + m2 = 0 vô nghiệm khi:
Lời giải
Chọn B
Ví dụ 3: Cho phương trình x4 - 2(m + 1)x2 + 2m + 3 = 0 là tham số. Tìm số tự nhiên m nhỏ nhất để phương trình có bốn nghiệm phân biệt.
Lời giải
Chọn A
Bài viết liên quan
- Tìm m để phương trình có nghiệm thỏa mãn điều kiện cho trước cực hay, có đáp án
- Các dạng bài tập về phương trình bậc hai một ẩn cực hay, có đáp án
- Cách giải phương trình chứa ẩn ở mẫu cực hay, có đáp án
- Cách giải phương trình tích cực hay, có đáp án
- Các dạng bài tập Phương trình quy về phương trình bậc hai cực hay, có đáp án
