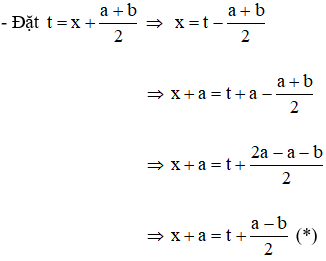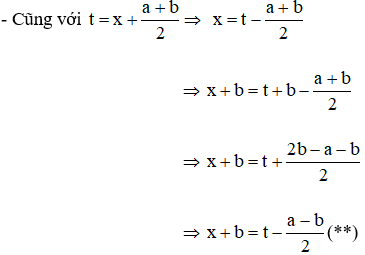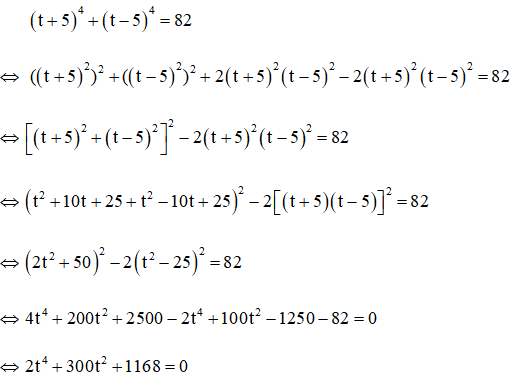Cách giải phương trình bậc bốn bằng cách đặt t (dạng (x + a)4 + (x + b)4 = c)
Với Cách giải phương trình bậc bốn bằng cách đặt t (dạng (x + a)4 + (x + b)4 = c) Toán học lớp 9 với đầy đủ lý thuyết, phương pháp giải và bài tập có lời giải cho tiết sẽ giúp học sinh nắm được Cách giải phương trình bậc bốn bằng cách đặt t (dạng (x + a)4 + (x + b)4 = c).
Cách giải phương trình bậc bốn bằng cách đặt t (dạng (x + a)4 + (x + b)4 = c)
A. Phương pháp giải
- Thay (*) và (**) vào phương trình biến đổi đưa về phương trình trùng phương
B. Bài tập
Câu 1: Giải phương trình (x - 6)4 + (x – 2)4 = -224 (1)
Giải
Đặt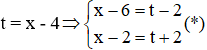 
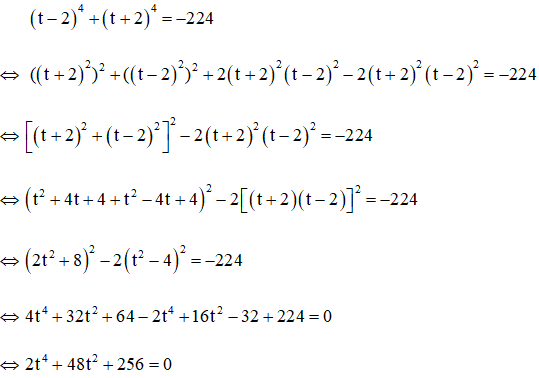
. Thay (*) vào phương trình (1) ta được
(không thỏa mãn điều kiện a ≥ 0)
Đặt a = t2 (a ≥ 0). Khi đó phương trình trở thành: 2a2 + 48a + 256 = 0
⇔ a2 + 24a + 128 = 0
(không thỏa mãn điều kiện a ≥ 0)
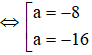
Vậy phương trình vô nghiệm
Câu 2: Giải phương trình (x + 1)4 + (x + 3)4 = 2 (1)
Giải
Đặt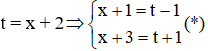 
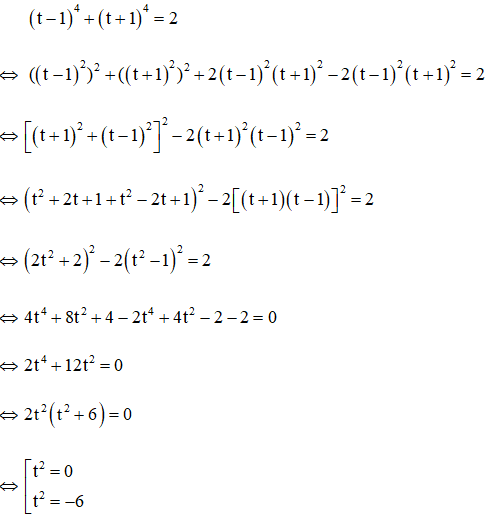
. Thay (*) vào phương trình (1) ta được
(không thỏa mãn điều kiện a ≥ 0)
Với t2 = 0 ⇒ t = 0 ⇒ x + 2 = 0 ⇔ x = -2
Với t2 = -6 (phương trình vô nghiệm)
Vậy phương trình có nghiệm duy nhất x = -2
Câu 3: Giải phương trình (x - 1)4 + (x – 7)4 = 0 (1)
Giải
Đặt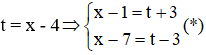 
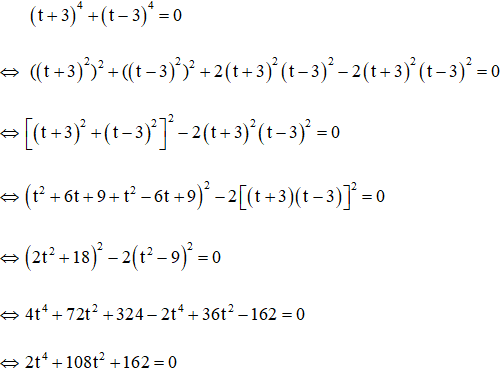
. Thay (*) vào phương trình (1) ta được
(không thỏa mãn điều kiện a ≥ 0)
Đặt a = t2 (a ≥ 0). Khi đó phương trình trở thành: 2a2 + 108a + 162 = 0
⇔ a2 + 54a + 81 = 0
(không thỏa mãn điều kiện a ≥ 0)
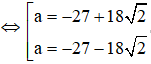
Vậy phương trình vô nghiệm.
Câu 4: Giải phương trình (x + 6)4 + (x – 4)4 = 82 (1)
Giải
Đặt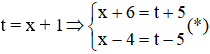 
. Thay (*) vào phương trình (1) ta được
Đặt a = t2 (a ≥ 0). Khi đó phương trình trở thành: 2a2 + 300a + 1168 = 0
(không thỏa mãn điều kiện a ≥ 0)
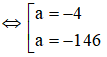
Vậy phương trình vô nghiệm
Câu 5: Giải phương trình (x + 3)4 + (x + 5)4 = 2 (1)
Giải
Đặt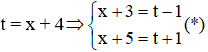 
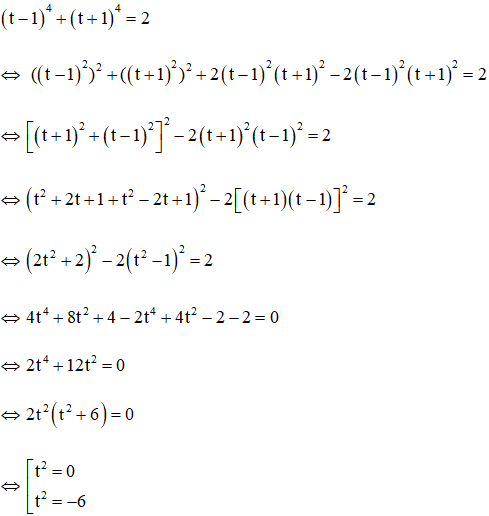
. Thay (*) vào phương trình (1) ta được
(không thỏa mãn điều kiện a ≥ 0)
Với t2 = 0 ⇒ t = 0 ⇒ x + 4 = 0 ⇔ x = -4
Với t2 = -6 (phương trình vô nghiệm)
Vậy phương trình có nghiệm duy nhất x = -4
Bài viết liên quan
- Tìm m để phương trình trùng phương vô nghiệm, có 1, 2, 3, 4 nghiệm
- Cách giải phương trình bậc bốn bằng cách đặt t (dạng (x + a)(x + b)(x + c)(x + d) = 0)
- Cách giải phương trình bậc bốn dạng ax^4 + bx^3 + cx ^2 ± kbx + k^2a = 0
- Cách giải phương trình chứa căn thức lớp 9 cực hay
- Cách giải phương trình có chứa dấu giá trị tuyệt đối hay, chi tiết
