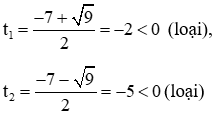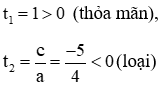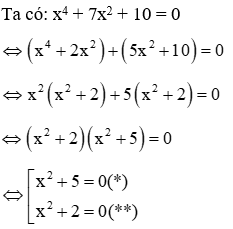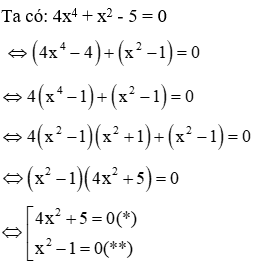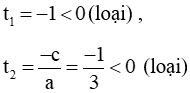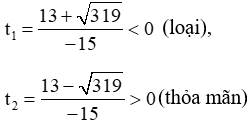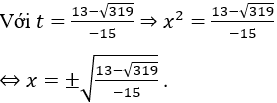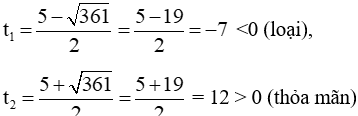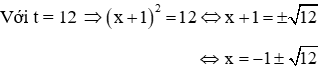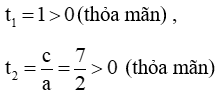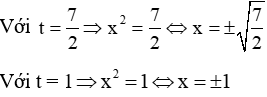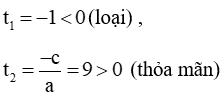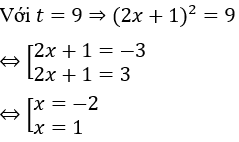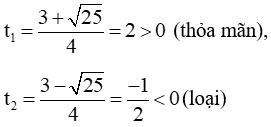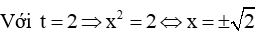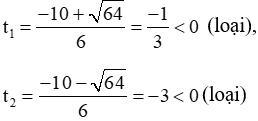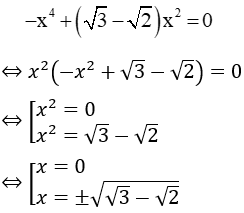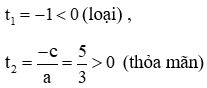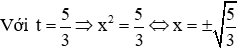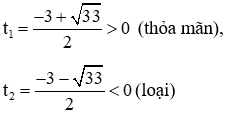Phương pháp giải phương trình trùng phương cực hay

A. Phương pháp giải

1. Phương pháp đặt ẩn phụ

Cho phương trình ax⁴ + bx² + c = 0 (a ≠ 0)   (1)

B1: Đặt t = x² (t ≥ 0). Phương trình (1) trở thành: at² + bt + c = 0 (a ≠ 0)   (2)

B2: Giải phương trình (2) tìm t, lấy nghiệm t thỏa mãn điều kiện (t ≥ 0)

B3: Với mỗi giá trị t tìm được ở B2 thay vào đẳng thức t = x² tìm x

Ví dụ 1: Giải phương trình x⁴ + 7x² + 10 = 0  (1)

Giải

Đặt t = x² (t ≥ 0). Phương trình (1) trở thành: t² + 7t + 10 = 0 (2)

Ta có: ∆ = 7² – 4.1.10 = 49 – 40 = 9 > 0

Vậy phương trình (2) có 2 nghiệm phân biệt:

Vậy phương trình (1) vô nghiệm

Ví dụ 2: Giải phương trình 4x⁴ + x² - 5 = 0  (1)

Giải

Đặt t = x² (t ≥ 0). Phương trình (1) trở thành: 4t² + t - 5 = 0 (2)

(2) là phương trình bậc hai có: a + b + c = 0 nên có 2 nghiệm phân biệt

Với t = 1 thì 1 = x² ⇔ x = ± 1

Vậy phương trình (1) có 2 nghiệm: x = 1, x = -1

2. Phương pháp đưa về phương trình tích

Ví dụ 1: Giải phương trình  x⁴ + 7x² + 10 = 0  (1)

Giải

Hai phương trình (*) và (**) vô nghiệm nên phương trình (1) vô nghiệm

Ví dụ 2: Giải phương trình 4x⁴ + x² - 5 = 0  (1)

Giải

Phương trình (*) vô nghiệm

Phương trình (**) ⇔ x² = 1 ⇔ x = ±1.

Vậy phương trình (1) có 2 nghiệm x = ±1

B. Bài tập

Câu 1: Số nghiệm của phương trình: 3x⁴ + 4x² + 1 = 0 (1) là

A.   0

B. 1

C. 2

D. 4

Giải

Đặt t = x² (t ≥ 0). Phương trình (1) trở thành: 3t² + 4t + 1 = 0 (2)

Phương trình (2) có a – b + c = 0 nên phương trình có 2 nghiệm

Vậy phương trình (1) vô nghiệm

Đáp án đúng là A

Câu 2: Số nghiệm của phương trình: -15x⁴ - 26x² + 10 = 0 (1) là

A.   1

B. 2

C. 3

D. 4

Giải

Đặt t = x² (t ≥ 0). Phương trình (1) trở thành: -15t² - 26t +10 = 0 (2)

Ta có: ∆ꞌ = (-13)² – (-15).10 = 169 + 150 = 319 > 0

Vậy phương trình (2) có 2 nghiệm phân biệt:

Vậy phương trình có 2 nghiệm

Đáp án đúng là B

Câu 3: Số nghiệm của phương trình: (x+1)⁴ – 5(x+1)² - 84 = 0 là

A.   0

B. 1

C. 2

D. 4

Giải

Đặt t = (x + 1)² (t ≥ 0). Phương trình (1) trở thành: t² - 5t - 84 = 0 (2)

Ta có: ∆ = (-5)² – 4.1.(-84) = 25 + 336 = 361 > 0

Vậy phương trình (2) có 2 nghiệm phân biệt:

Vậy phương trình có 2 nghiệm

Đáp án đúng là C

Câu 4: Số nghiệm của phương trình: 2x⁴ - 9x² + 7 = 0 (1) là

A.   0

B. 1

C. 2

D. 4

Giải

Đặt t = x² (t ≥ 0). Phương trình (1) trở thành: 2t² - 9t + 7 = 0 (2)

Phương trình (2) có a + b + c = 0 nên phương trình có 2 nghiệm

Vậy phương trình có 4 nghiệm

Đáp án đúng là D

Câu 5: Tích các nghiệm của phương trình: (2x + 1)⁴ – 8(2x + 1)² - 9 = 0 là

A.   2

B. 4

C. -2

D. -4

Giải

Đặt t = (2x + 1)² (t ≥ 0). Phương trình (1) trở thành: t² - 8t - 9 = 0 (2)

Phương trình (2) có a – b + c = 0 nên phương trình có 2 nghiệm

Vậy tích các nghiệm của phương trình là -2.

Đáp án đúng là C

Câu 6: Số nghiệm dương của phương trình  2x⁴ - 3x² - 2 = 0 (1) là

A.   0

B. 1

C. 2

D. 3

Giải

Đặt t = x² (t ≥ 0). Phương trình (1) trở thành: 2t² - 3t - 2 = 0 (2)

Ta có: ∆ = (-3)² – 4.2.(-2) = 9 + 16 = 25 > 0

Vậy phương trình (2) có 2 nghiệm phân biệt:

Vậy phương trình có 1 nghiệm dương

Đáp án đúng là B

Câu 7: Số nghiệm âm của phương trình: 3x⁴ + 10x² + 3 = 0 là

A.   0

B. 1

C. 2

D. 4

Giải

Đặt t = x² (t ≥ 0). Phương trình (1) trở thành: 3t² + 10t + 3 = 0 (2)

Ta có: ∆ = (10)² – 4.3.3 = 100 - 36 = 64 > 0

Vậy phương trình (2) có 2 nghiệm phân biệt:

Vậy phương trình (1) có vô nghiệm, do đó (1) không có nghiệm âm nào

Đáp án đúng là A

Câu 8: Số nghiệm của phương trình: 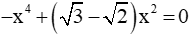 là

A. 3

B. 1

C. 2

D. 4

Giải

Ta có:    

Vậy phương trình có 3 nghiệm

Đáp án đúng là A

Câu 9: Số nghiệm của phương trình: 3x⁴ - 2x² - 5 = 0 (1) là

A. 0

B. 1

C. 2

D. 4

Giải

Đặt t = x² (t ≥ 0). Phương trình (1) trở thành: 3t² - 2t - 5 = 0 (2)

Phương trình (2) có a – b + c = 0 nên phương trình có 2 nghiệm

Vậy phương trình có 2 nghiệm

Đáp án đúng là C

Câu 10: Số nghiệm lớn hơn 1 của phương trình: x⁴ + 3x² - 6 = 0 (1) là

A.   0

B. 1

C. 2

D. 3

Giải

Đặt t = x² (t ≥ 0). Phương trình (1) trở thành: t² + 3t - 6 = 0 (2)

Ta có: ∆ = 3² – 4.1.(-6) = 9 + 24 = 33 > 0

Vậy phương trình (2) có 2 nghiệm phân biệt:

Vậy phương trình có một nghiệm lớn hơn 1

Đáp án đúng là B