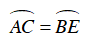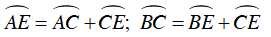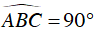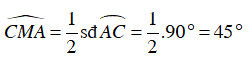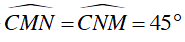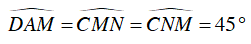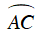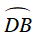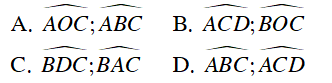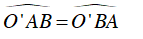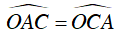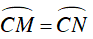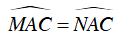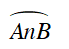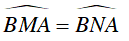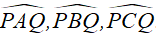Các dạng bài tập về Góc nội tiếp chọn lọc, có lời giải

A. Phương pháp giải

Ta áp dụng các kiến thức sau:

1. Góc nội tiếp là góc có đỉnh nằm trên đường tròn và hai cạnh chứa hai dây cung của đường tròn đó.

Cung nằm bên trong góc gọi là cung bị chắn.

2. Trong một đường tròn, số đo của góc nội tiếp bằng một nửa số đo của cung bị chắn.

3. Trong một đường tròn:

a) Các góc nội tiếp bằng nhau chắn các cung bằng nhau.

b) Các góc nội tiếp cùng chắn một cung hoặc chắn các cung bằng nhau thì bằng nhau.

c) Góc nội tiếp (nhỏ hơn hoặc bằng) có số đo bằng nửa số đo của góc ở tâm cùng chắn một cung.

d) Góc nội tiếp chắn nửa đường tròn là góc vuông.

B. Ví dụ minh họa

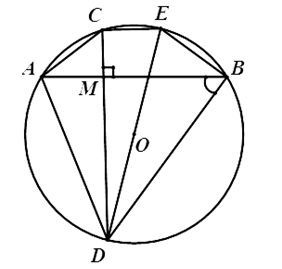
Ví dụ 1 : Cho đường tròn (O; R) và một điểm M bên trong đường tròn đó. Qua M kẻ hai dây cung AB và CD vuông góc với nhau (C thuộc cung nhỏ AB). Vẽ đường kính DE. Chứng minh rằng:

a) MA.MB = MC.MD.

b) Tứ giác ABEC là hình thang cân.

c) Tổng MA² + MB² + MC² + MD² có giá trị không đổi khi M thay đổi vị trí trong đường tròn (O).

Hướng dẫn giải

a) Xét ΔAMC và ΔDMB có:

 ( hai góc nội tiếp cùng chắn cung  )

 (GT)

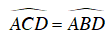
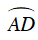
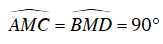
⇒ ΔAMC ∼ ΔDMB (g.g)

⇒ MA/MD = MC/MB ⇔ MA.MB = MC.MD.

b) Ta có: 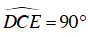 (góc nội tiếp chắn nửa đường tròn)

⇒ CD ⊥ CE

Mà CD ⊥ AB (gt)

⇒ AB // CE.

⇒ Tứ giác ABEC là hình thang (1).

Mặt khác: CE và AB là hai dây song song của đường tròn (O) chắn hai cung AC và BE nên 

Ta lại có: 

 .(hai góc nội tiếp chắn hai cung bằng nhau) (2)

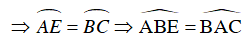
Từ (1) và (2) suy ra tứ giác ABEC là hình thang cân.

c) Vì 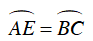 (chứng minh trên)

⇒ AE = BC .

Mặt khác: 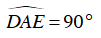 (góc nội tiếp chắn nửa đường tròn)

Xét vuông tại A có: AD² + AE² = DE² (định lý Py – ta – go)

Xét tổng: MA² + ² + MC² + MD²

= (MA² + MD²) + (MB² + MC²)

= AD² + BC² = AD² + AE² = DE² = 4R² không đổi.

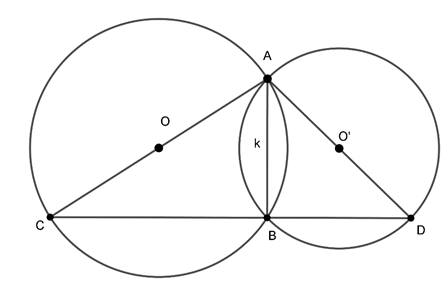
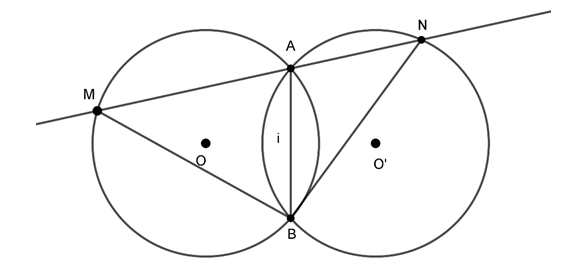
Ví dụ 2 : Cho hai đường tròn (O) và (O’) cắt nhau tại A và B. Vẽ các đường kính AC, AD của hai đường tròn. Chứng minh ba điểm C, B, D thẳng hàng.

Hướng dẫn giải

Ta có: Trong đường tròn tâm O, 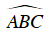 là góc nội tiếp chắn nửa đường tròn

⇒ 

Trong đường tròn tâm O’, 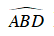 là góc nội tiếp chắn nửa đường tròn

Suy ra, ba điểm C, B và D thẳng hàng.

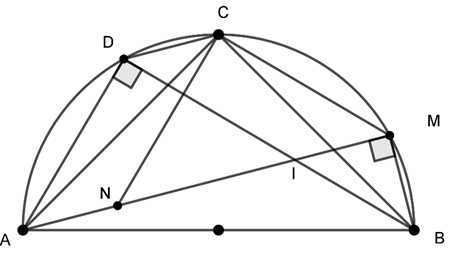
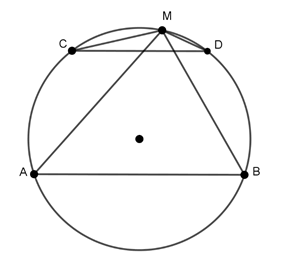
Ví dụ 3 : Cho nửa đường tròn (O) đường kính AB và C là điểm chính giữa của cung AB. Lấy điểm M thuộc cung BC và điểm N thuộc tia AM sao cho AN = BM. Kẻ dây CD song song với AM.

a) Chứng minh ΔACN = ΔBCM .

b) Chứng minh ΔCMN vuông cân.

c) Tứ giác ANCD là hình gì? Vì sao?

Hướng dẫn giải

a) Xét ΔACN và ΔBCM có:

AC = BC (vì C là điểm chính giữa cung AB)

 (hai góc nội tiếp cùng chắn cung  )

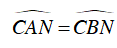
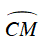
AN = BM (gt)

⇒ ΔACN = ΔBCM (c.g.c)

b) Vì ΔACN = ΔBCM (chứng minh a)

⇒ CN = CM ⇒ ΔCMN cân tại C (1)

⇒ (hai góc ở đáy)

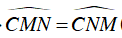
Lại có 

⇒ 

⇒ (2)

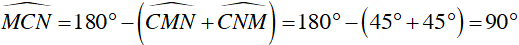
Từ (1) và (2) suy ra ΔCMN vuông cân tại C.

c) Vì CD // AM nên tứ giác ADCM là hình thang cân.

Ta có: 

Suy ra: AD // CN.

Vậy tứ giác ADCN là hình bình hành.

Ví dụ 4 : Cho đường tròn tâm O và hai dây cung song song AB, CD. Trên cung AB lấy điểm M. Chứng minh rằng  .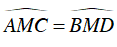

Hướng dẫn giải

Ta có:  là góc nội tiếp chắn 

 là góc nội tiếp chắn 

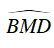
Ta lại có AB//CD nên  .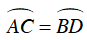

Do đó: 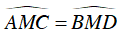 ( hai góc nội tiếp chắn hai cung bằng nhau).

Ví dụ 5 : Cho đường tròn (O) đường kính AB và hai điểm E, F nằm trên một đường tròn. Các đường thẳng AE, BF cắt nhau tại P nằm ngoài đường tròn (O). AF và BE cắt nhau tại Q. Chứng minh PQ vuông góc với AB.

Hướng dẫn giải

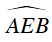
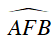
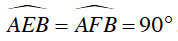
Ta có  và  là góc nội tiếp chắn nửa đường tròn nên  .

⇒ AF ⊥ PB, BE ⊥ PA

Xét ΔPAB , ta có: AF ⊥ PB, BE ⊥ PA

Mà AF ∩ BE = {Q}

Suy ra Q là trực tâm ΔPAB .

Từ đó suy ra PQ ⊥ AB .

C. Bài tập trắc nghiệm

Câu 1 : Cho đường tròn tâm O. Trên đường tròn lấy 4 điểm theo thứ tự A,B, C và D. Hỏi cặp góc nào sau đây bằng nhau

Hướng dẫn giải

Đáp án C

Ta có 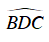 là góc nội tiếp chắn 

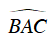
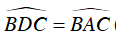
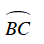
Và  là góc nội tiếp chắn 

⇒  ( hai góc nội tiếp cùng chắn  ).

Câu 2 : Cho hai đường tròn (O; R) và (O’; R’) tiếp xúc trong với nhau tại A, (R > R'). Qua điểm B bất kỳ trên (O’) vẽ tiếp tuyến với (O’) cắt (O) tại hai điểm M và N, AB cắt (O) tại C. Các phát biểu đúng là:

(I) MN ⊥ OC

(II) AC là tia phân giác của

(III) MN ⊥ AB

A. (I) và (III)

B. (II) và (III)

C. (I) và (III)

D. (I), (II) và (III)

Hướng dẫn giải

Đáp án C

+ Vì Δ O'AB cân tại O’ nên 

Δ OAC cân tại O nên 

Suy ra 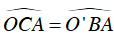 , mà hai góc này ở vị trí đồng vị, do đó O’B // OC.

Mặt khác MN là tiếp tuyến của (O’) tại B

⇒ O'B ⊥ MN. Do đó OC ⊥ MN

+ Trong đường tròn (O):

⇒ OC là đường trung trực của MN

⇒ CM = CN

⇒ 

⇒ 

Hay AC là tia phân giác của  .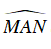

Câu 3 : Khẳng định nào sau đây là sai?

A. Trong một đường tròn, góc nội tiếp chắn nửa đường tròn là góc vuông

B. Trong một đường tròn, hai góc nội tiếp bằng nhau chắn hai cung bằng nhau

C. Trong một đường tròn, hai góc nội tiếp cùng chắn một cung thì bằng nhau

D. Trong một đường tròn, hai góc nội tiếp bằng nhau thì cùng chắn một cung

Hướng dẫn giải

Đáp án D

Vì trong một đường tròn, hai góc nội tiếp bằng nhau thì có thể chắn hai cung bằng nhau.

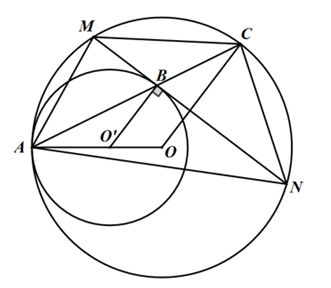
Câu 4 : Cho hai đường tròn bằng nhau (O) và (O’) cắt nhau tại A và B . Vẽ đường thẳng qua A cắt đường tròn (O) tại M và cắt đường tròn (O’) tại N (A nằm giữa M và N). Hỏi tam giác MNB là tam giác gì?

A. Tam giác cân

B. Tam giác đều

C. Tam giác vuông

D. Tam giác vuông cân

Hướng dẫn giải

Đáp án A

+ (O) và (O’) là hai đường tròn bằng nhau

 cùng được căng bởi dây AB

⇒  (1)

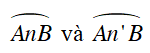
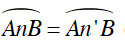
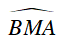
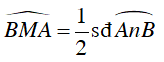
+ (O) có  là góc nội tiếp chắn cung 

⇒  (2)

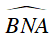
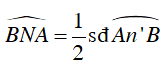
+ (O’) có  là góc nội tiếp chắn cung 

⇒  (2)

Từ (1); (2); và (3) suy ra 

⇒ ΔBMN cân tại B.

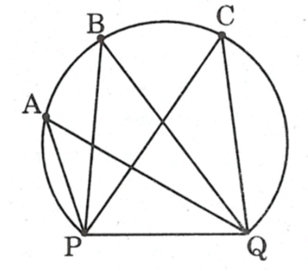
Câu 5 : Một huấn luyện viên cho cầu thủ tập sút bóng vào cầu môn PQ. Bóng được đặt ở các vị trí A, B, C trên một cung tròn như hình bên. Hãy so sánh các góc 

Hướng dẫn giải

Đáp án D

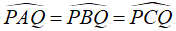
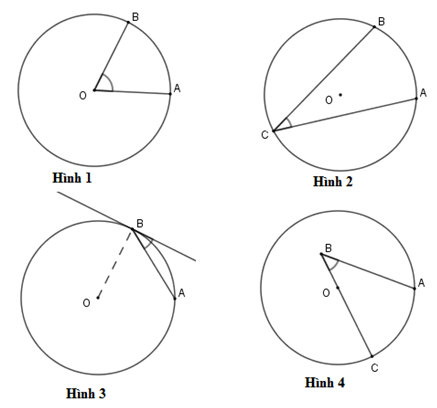
Ta có  vì chúng là các góc nội tiếp chắn cùng một cung 

Câu 6 : Hình nào dưới đây biểu diễn góc nội tiếp?

A. Hình 1

B. Hình 2

C. Hình 3

D. Hình 4

Hướng dẫn giải

Đáp án B

Hình 1: Góc 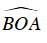 là góc ở tâm

Hình 2: Góc 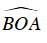 là góc nội tiếp

Hình 3: Có một cạnh không là dây của đường tròn

Hình 4 : Góc đã cho có đỉnh không nằm trên đường tròn

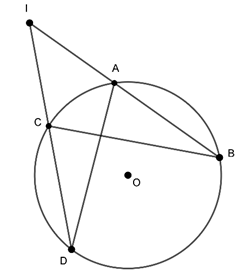
Câu 7 : Cho đường tròn (O) và điểm I nằm ngoài (O). Từ điểm I kẻ hai dây cung AB và CD (A nằm giữa I và B, C nằm giữa I và D)

Tích IA.IB bằng

A. ID.CD

B. IC.CB

C. IC.CD

D. ID.IC

Hướng dẫn giải

Đáp án D

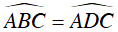
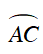
Ta có:  (hai góc nội tiếp cùng chắn  )

Xét ΔIAD và ΔICB , ta có:

 ( chứng minh trên)

 : góc chung

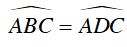
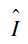
⇒ ΔIAD ∼ ΔICB (g – g)

⇒  .

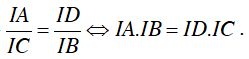
Vậy IA.IB = ID.IC .